A type of cellular automaton with the intent of simulating autopoiesis in an emergent manner, with a simple scaling rule and with each unit having binary state attribution and a corresponding gate associated to it. Such concept of autopoiesis is as introduced by Maturana and Varela in Autopoiesis and Cognition: The Realization of the Living, and also a bit developed in Principles of biological autonomy(1979) by Varela.
Autopoiesis can be viewed as the capacity of a system to generate and (re)build itself. Associated to this concept of autopoiesis is that of organizational closure or closure of constraints. These very briefly mean that any process (and respective constraints on it) needs to generate atleast another constraint. Here, processes and relations between them evolve in order to maintain such closure. Through this lens, any new adaptation or behaviour taken by an organism can be seen as a compensation to a pertubation (e.g. self-replication).
Alternatively to this emergent approach, some examples might be those of Varela’s model for the simulation of autopoiesis, Terrence Deacon’s simulation for his autogen, and more generally approaches which employ object calculi, for example using λ-calculus, Fontana’s & Buss’ abstract chemistry(although not directly applied to autopoiesis) being an example of that.
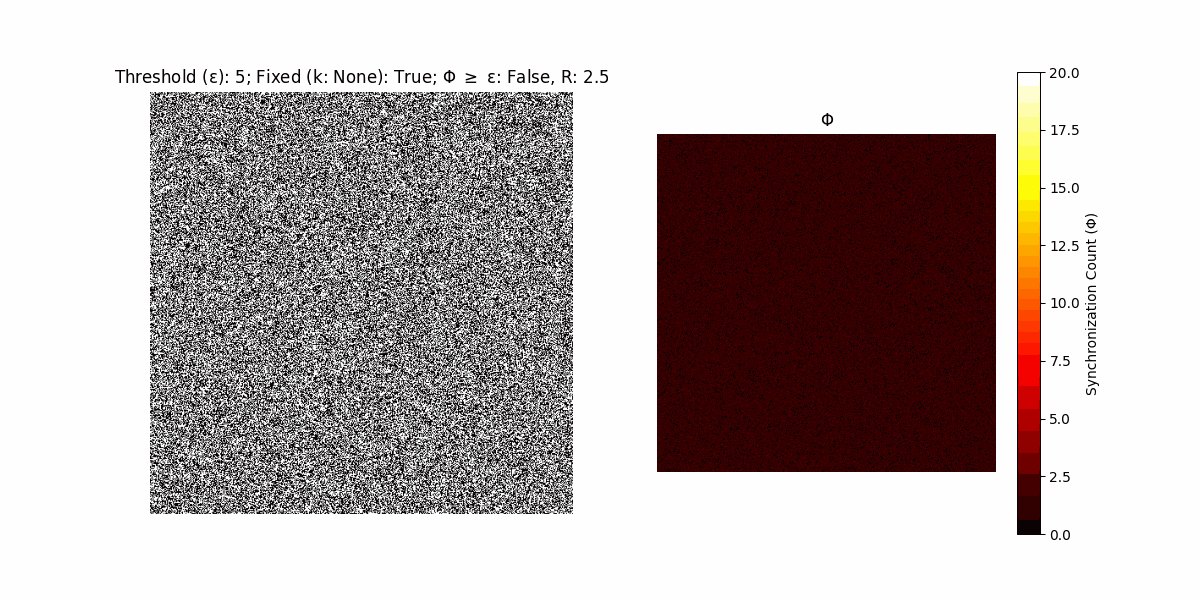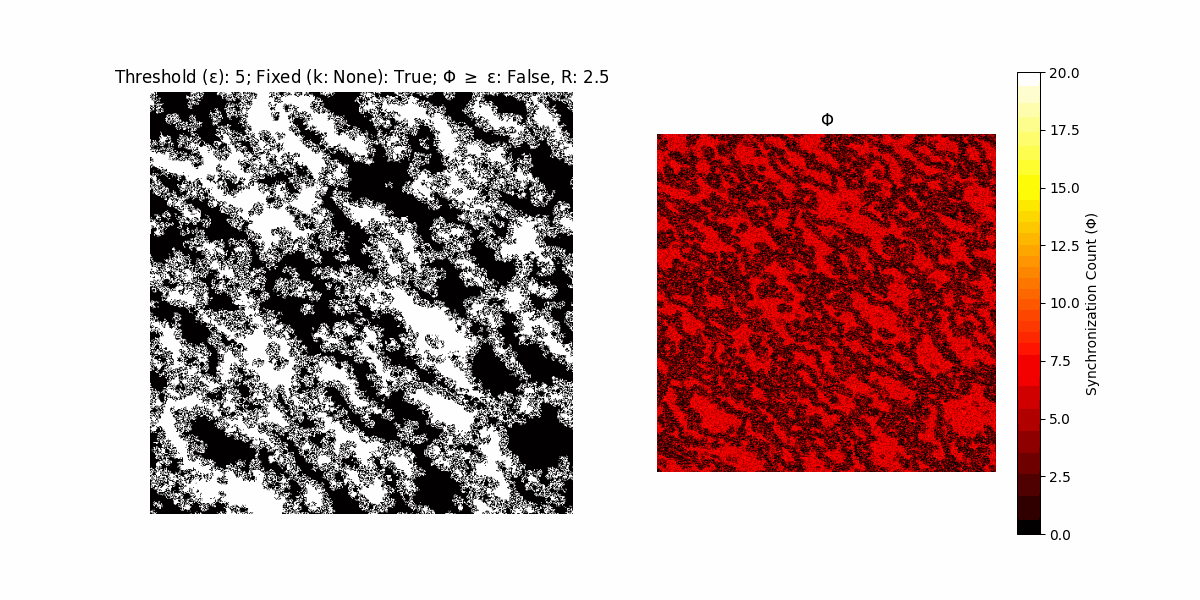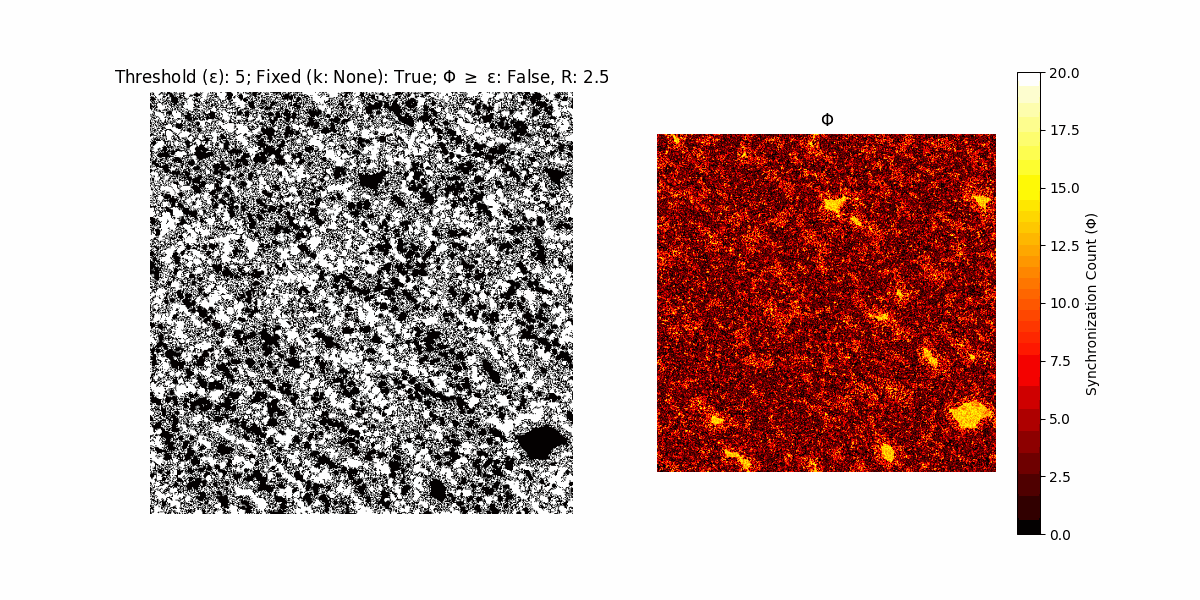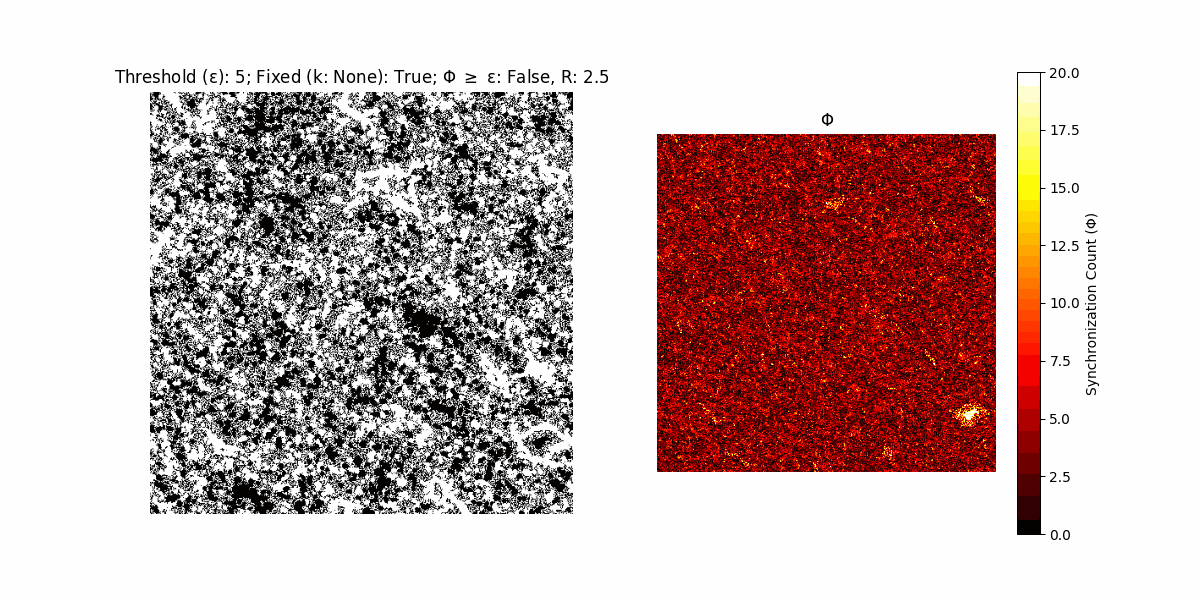
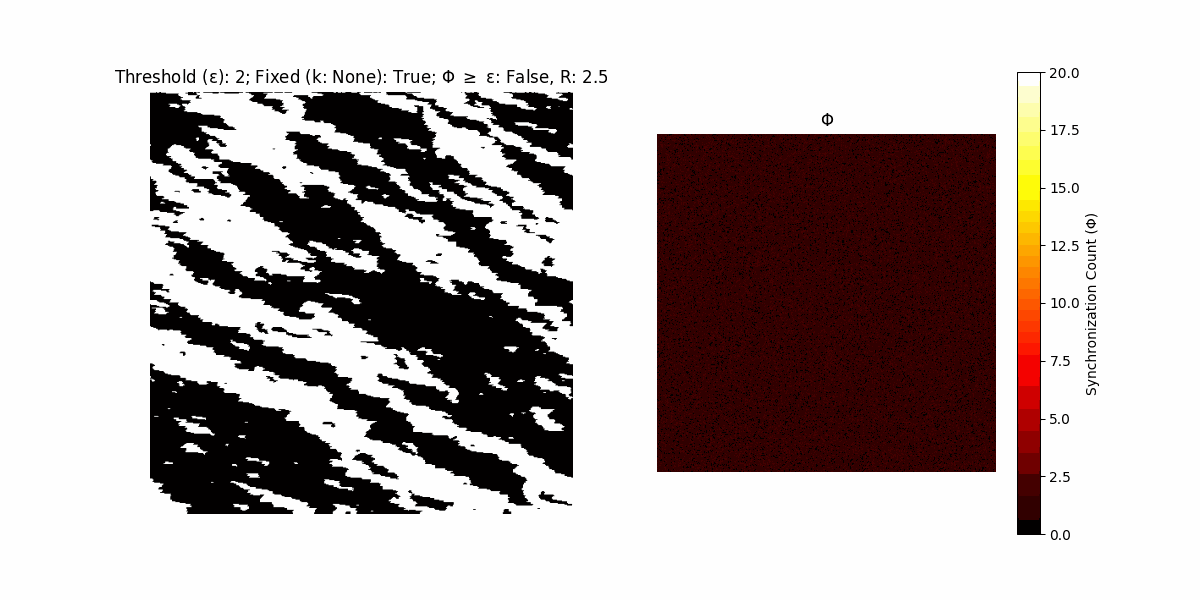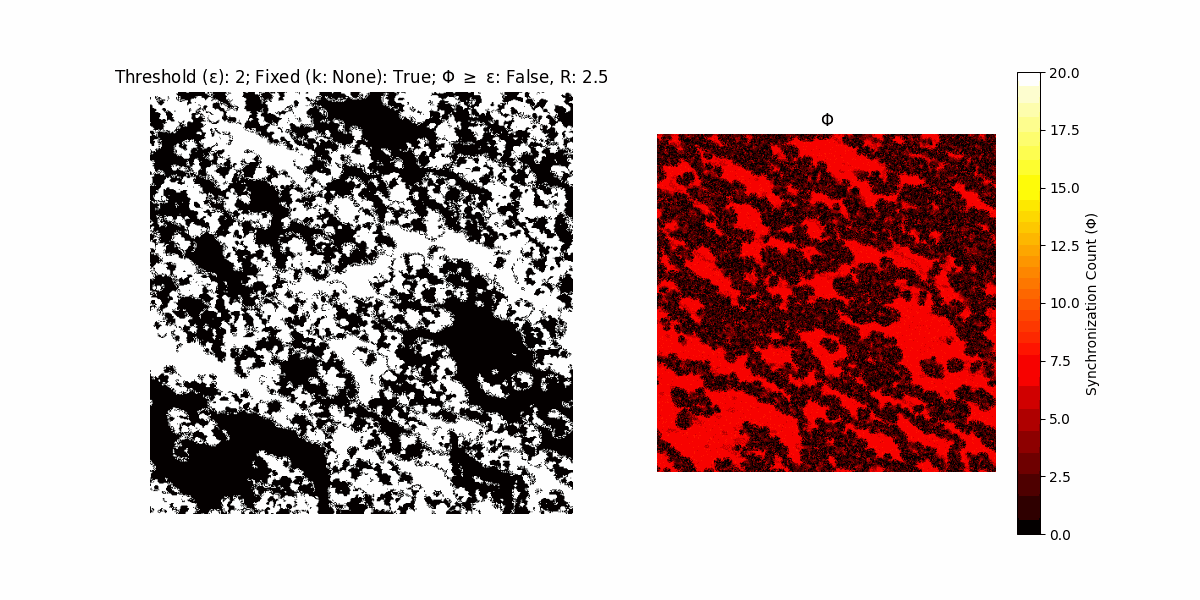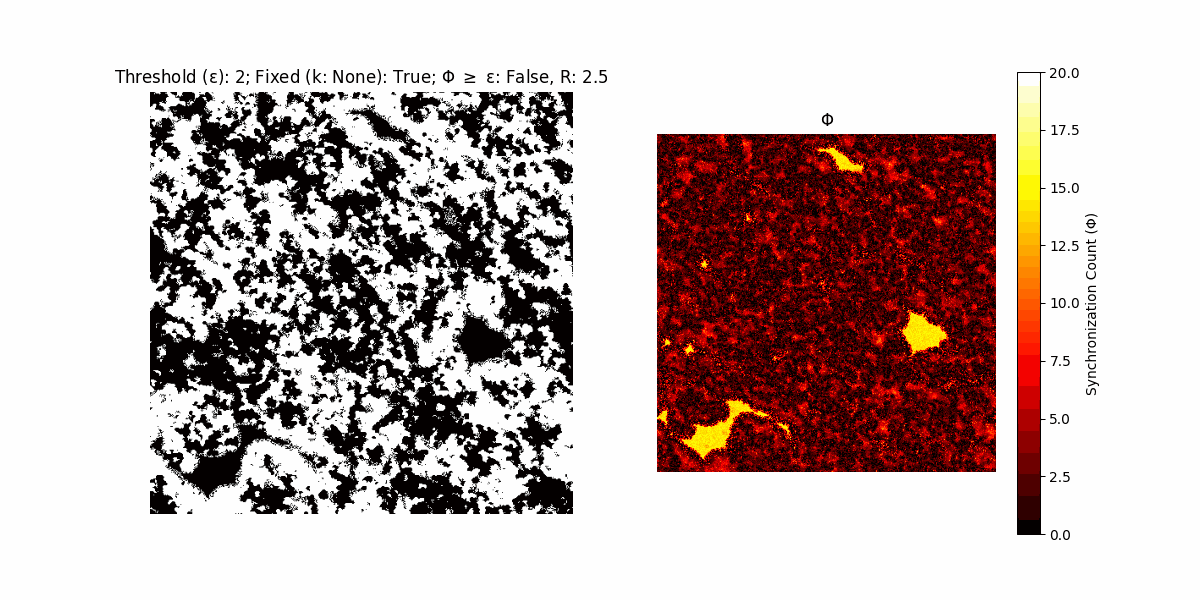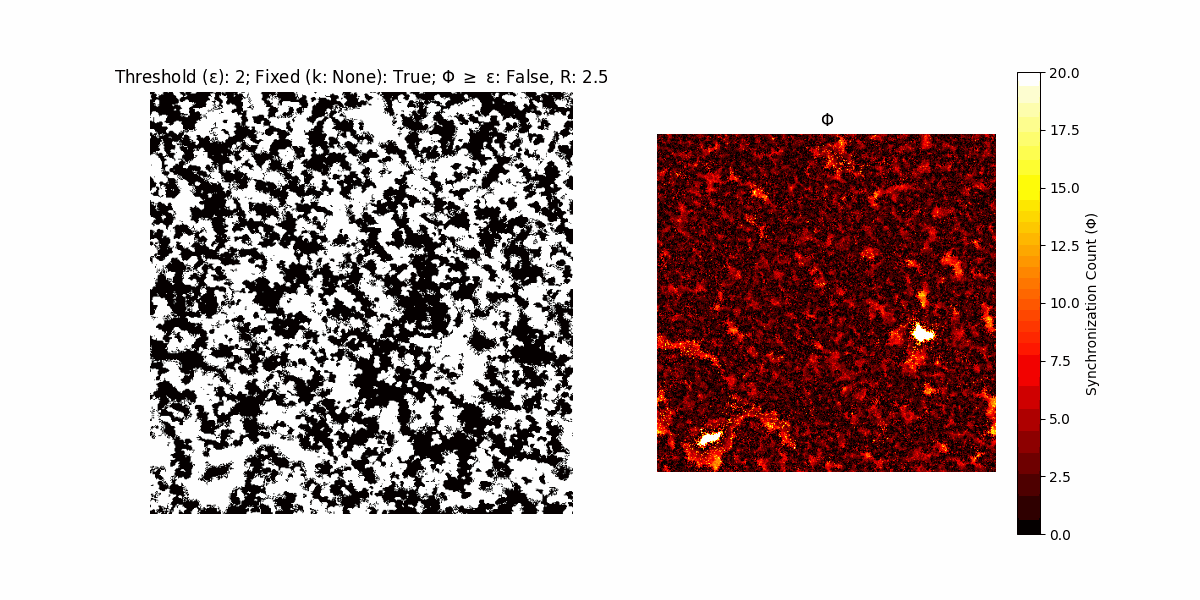
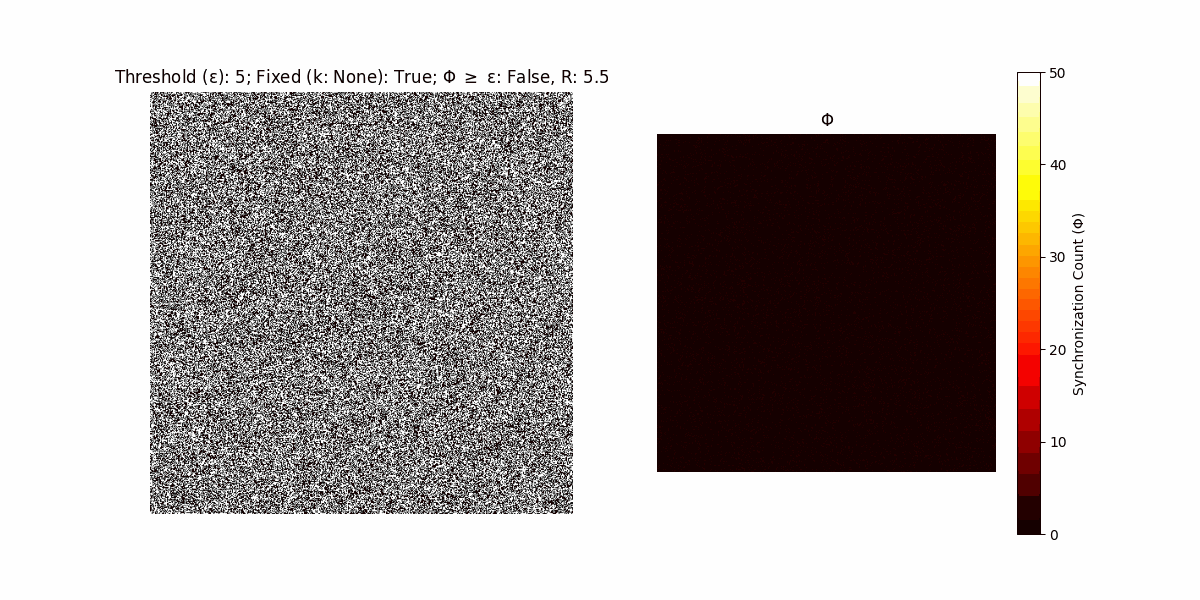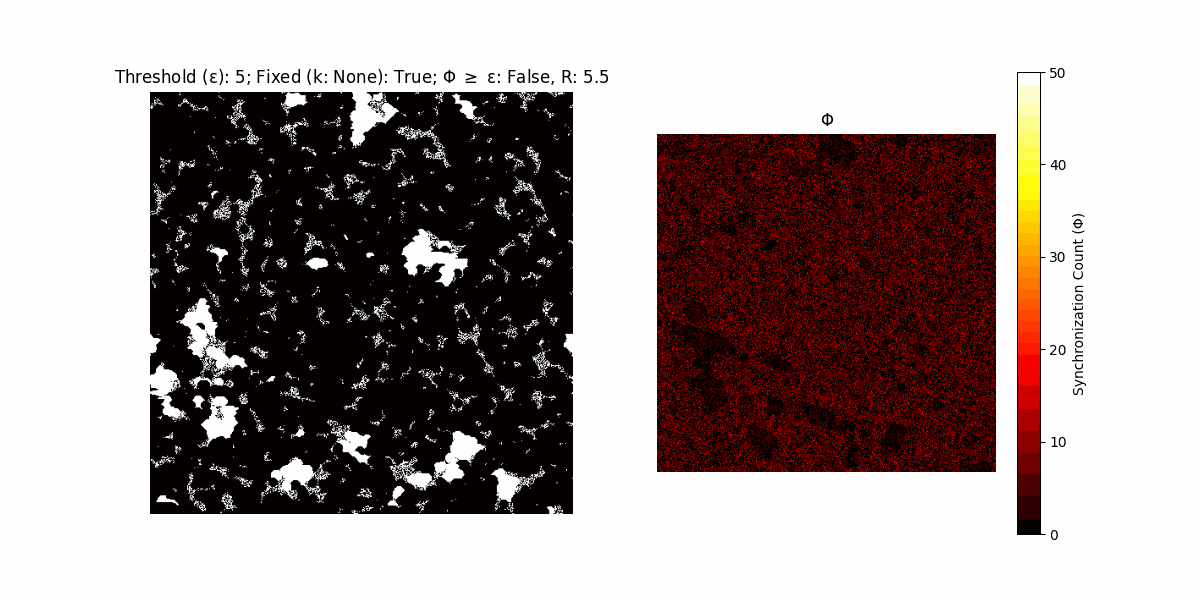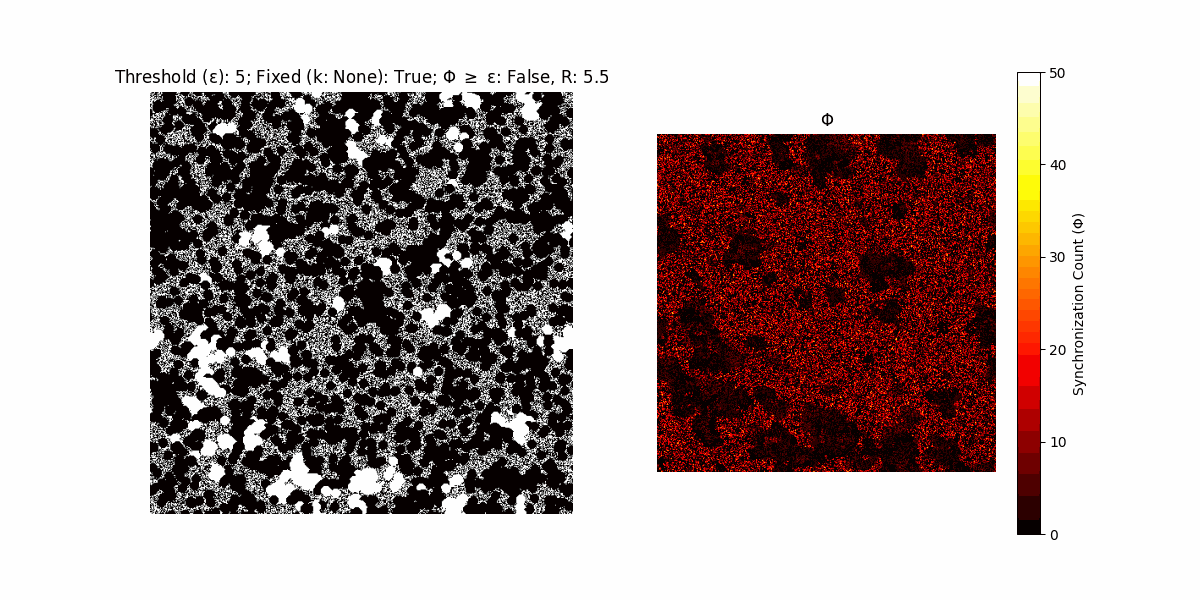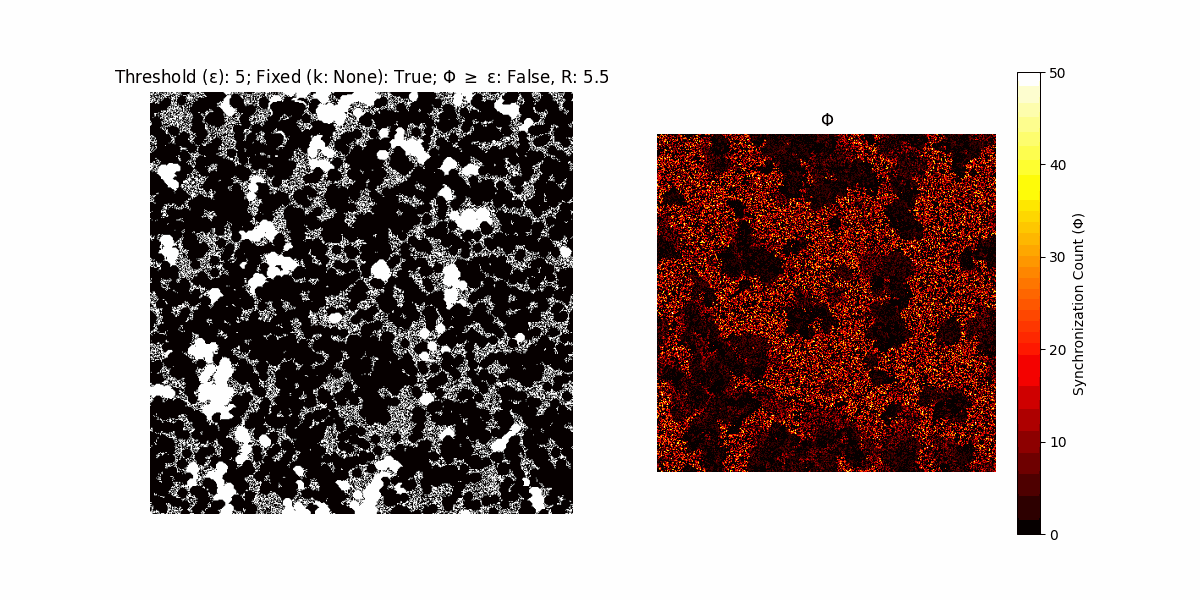
A network with N x N units is initialized, with each unit’s state $∈ {0, 1}$ being randomly assigned. Over each iteration (with a max of N_iter), there’s a logic gate randomly chosen from a set (examples with AND, OR and XOR), for the update of each unit’s state according to its neighbors’ states.
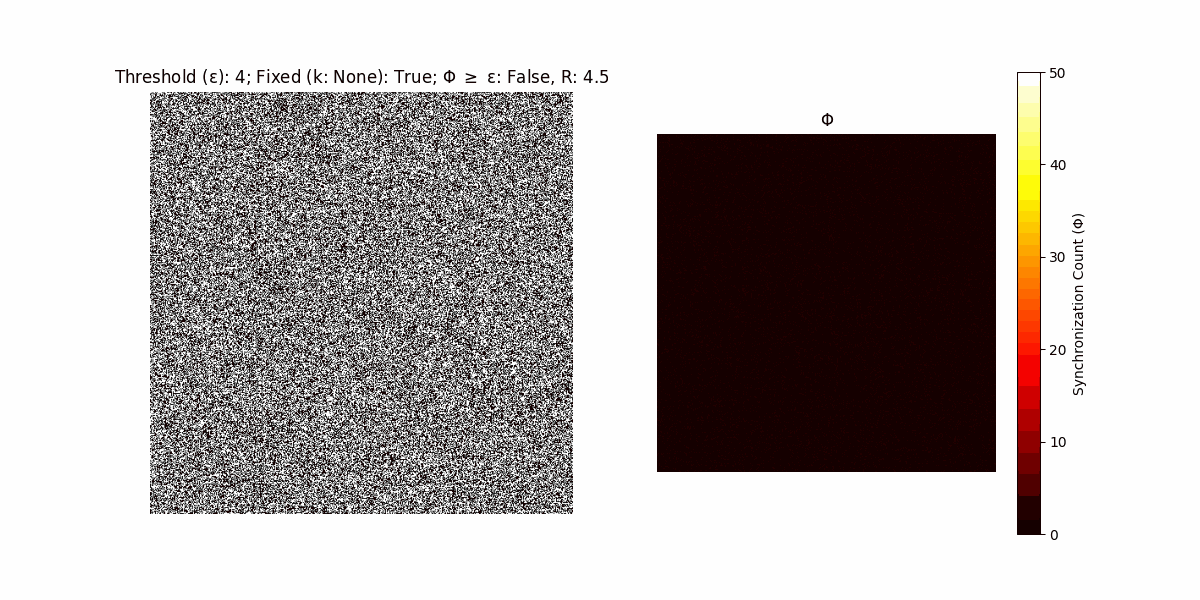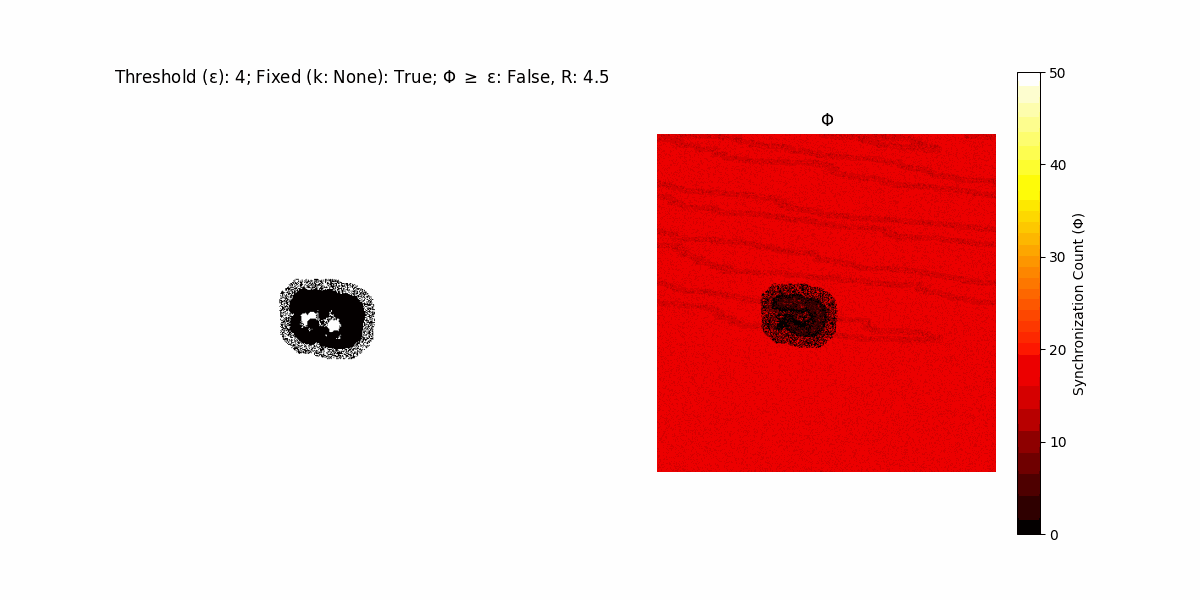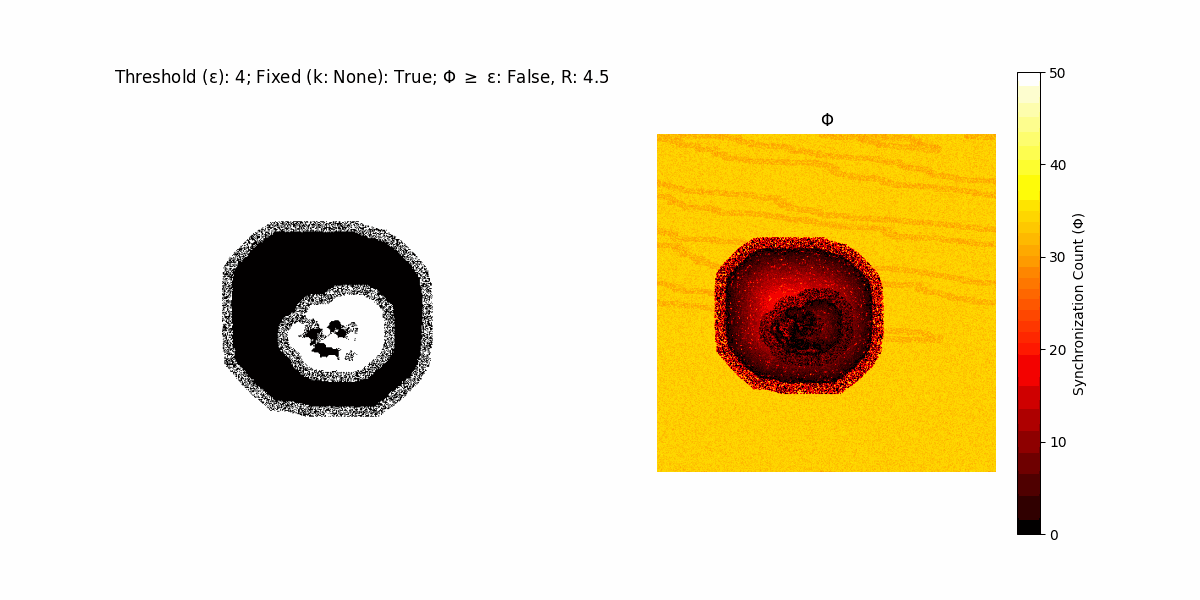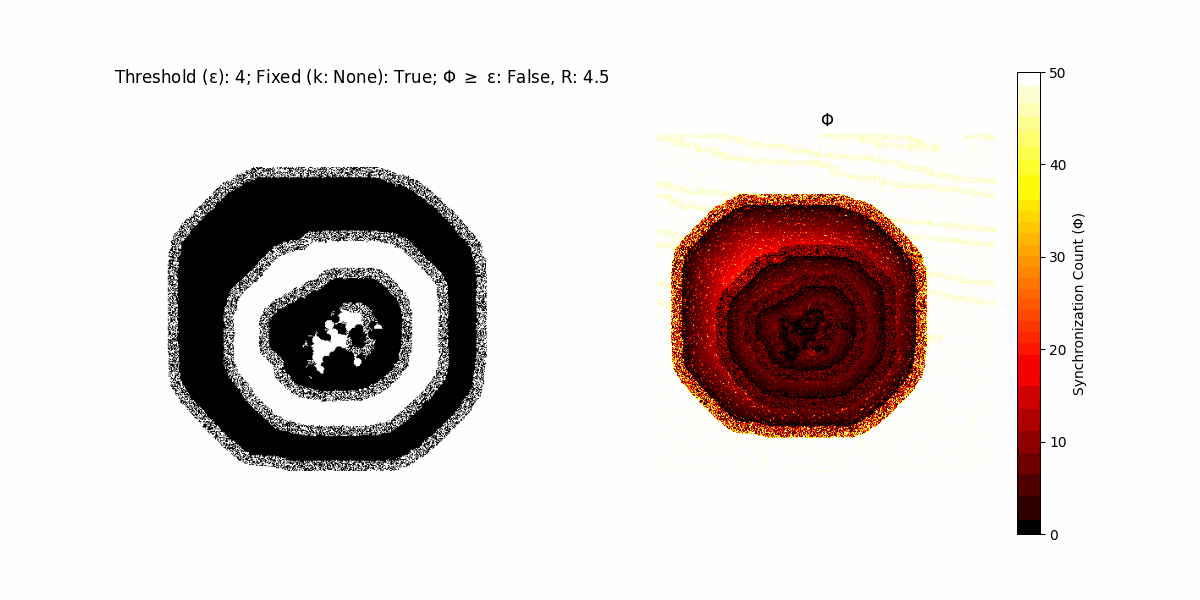
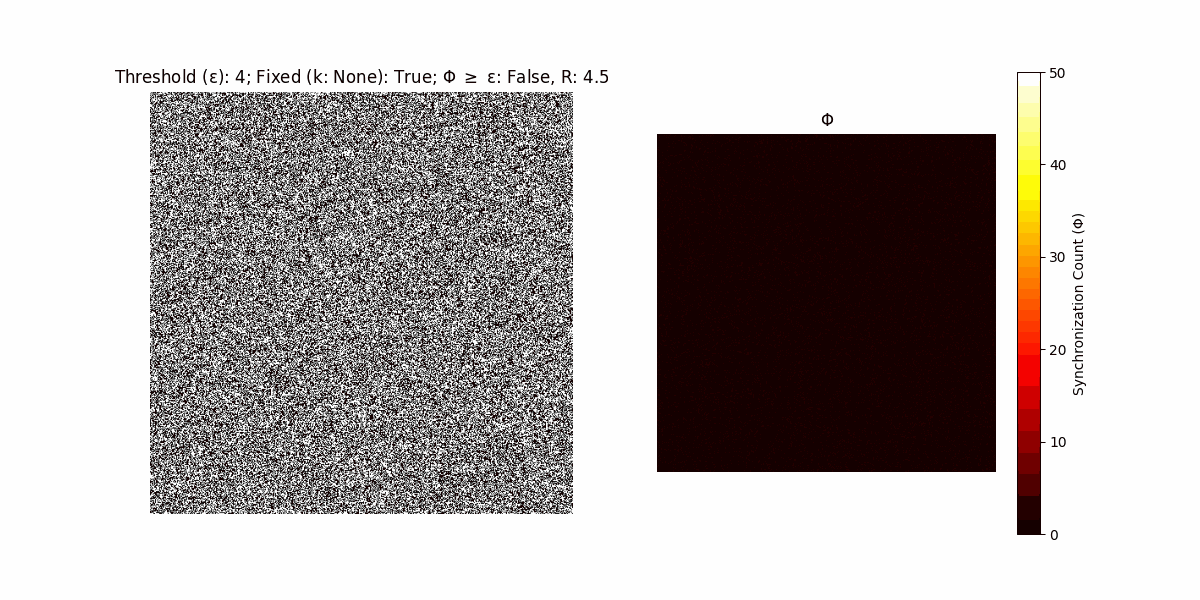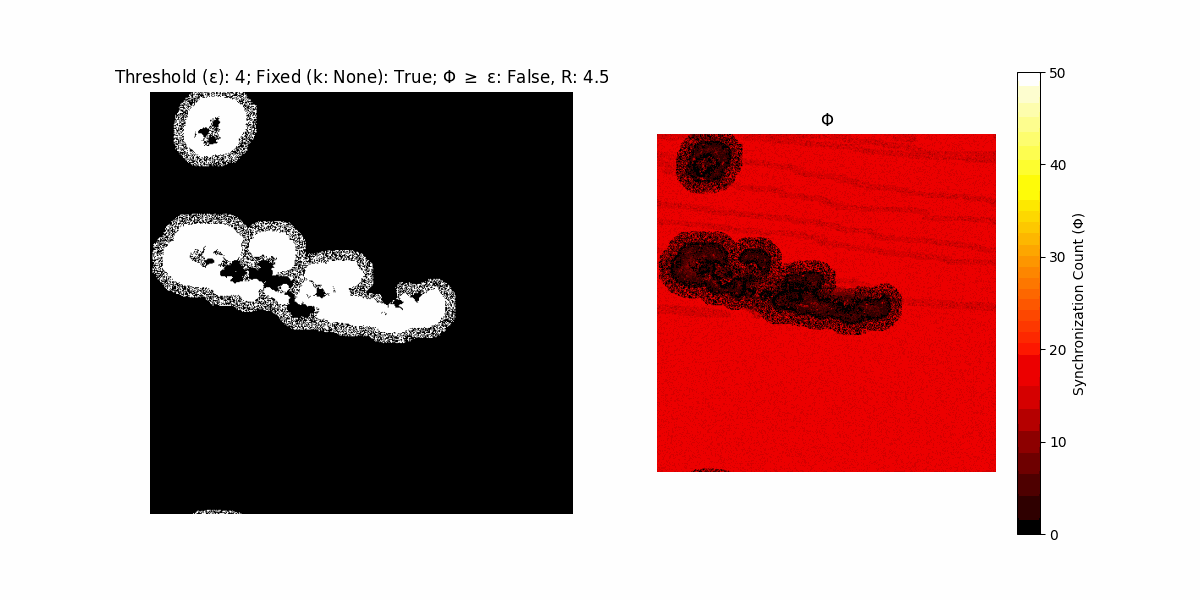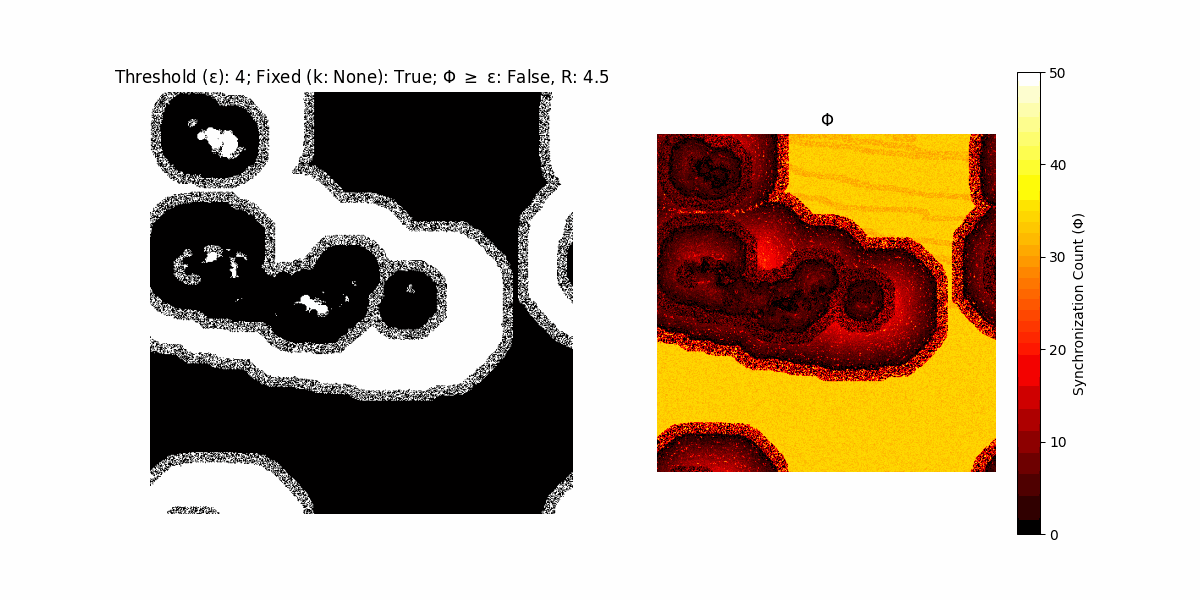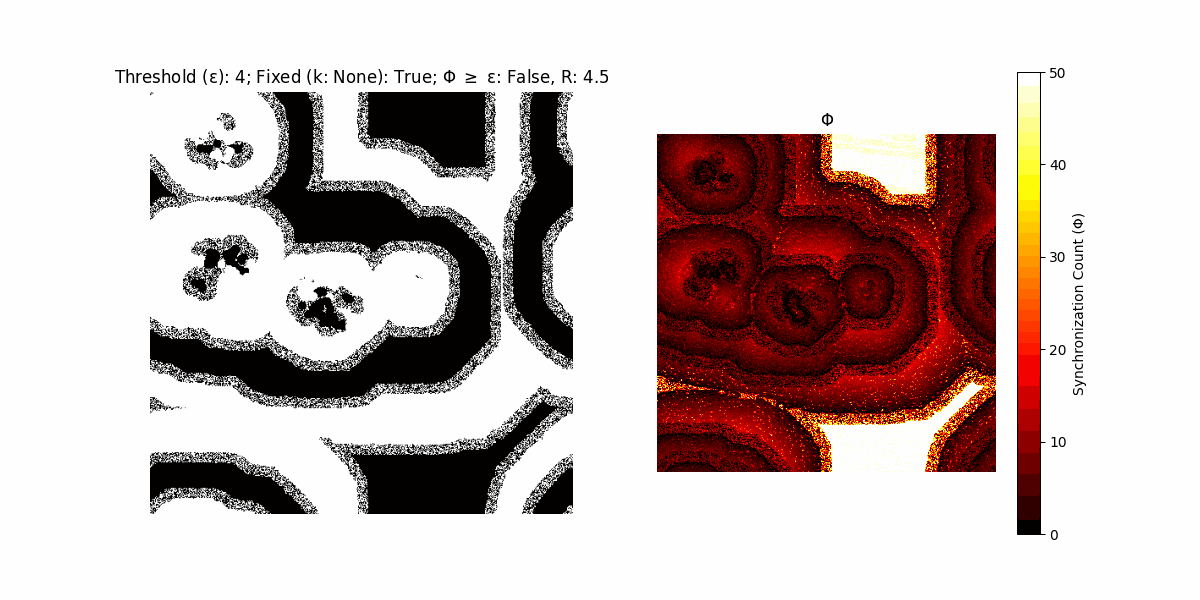
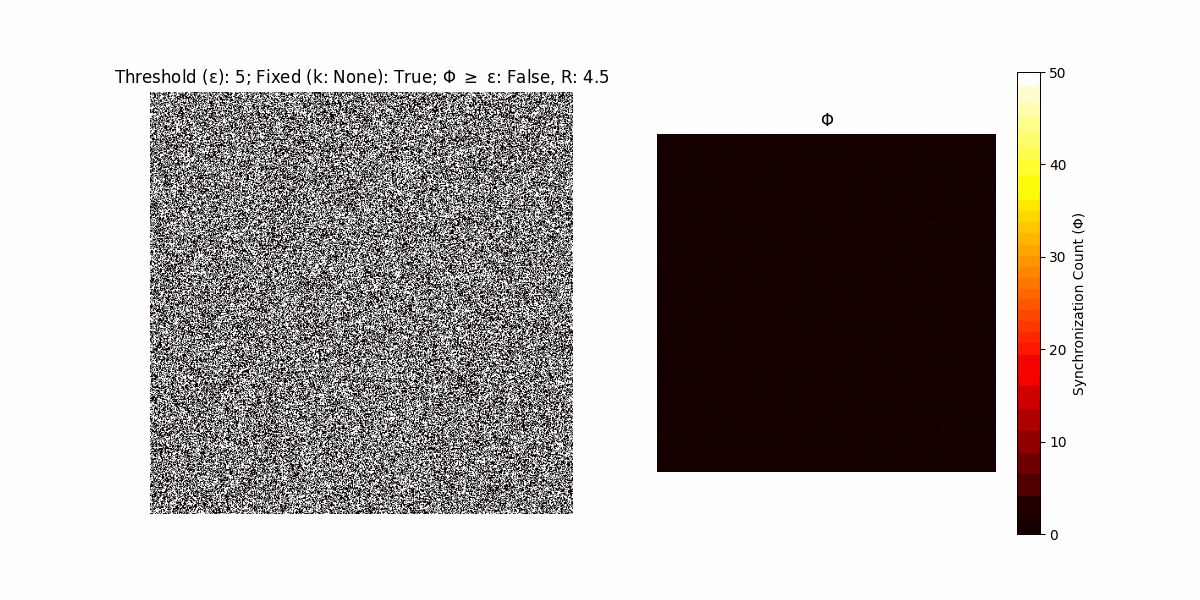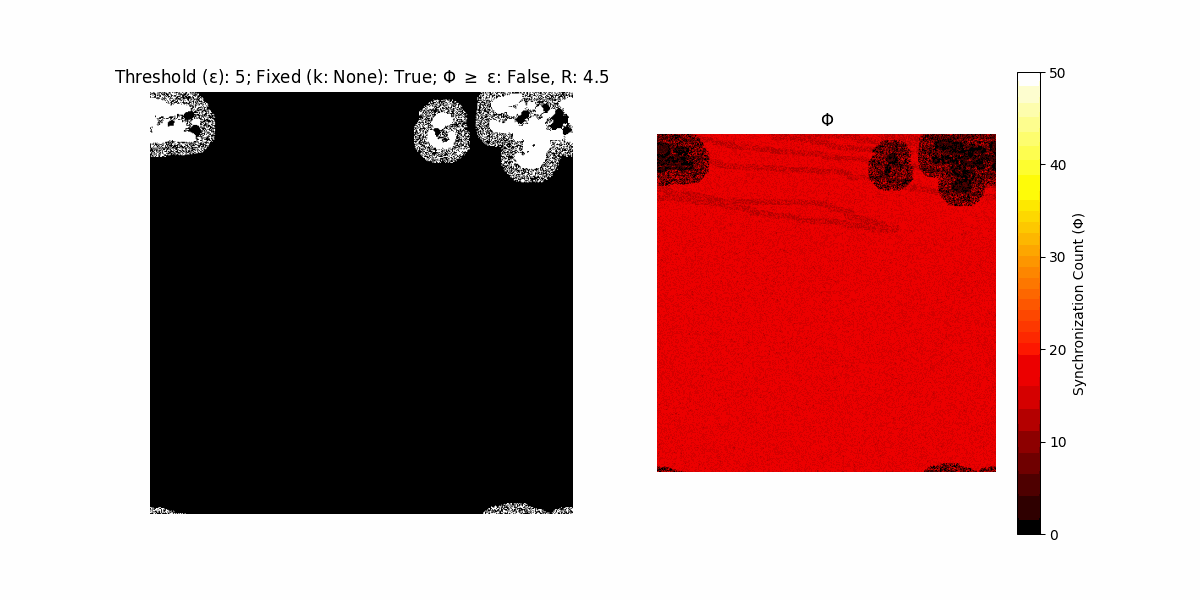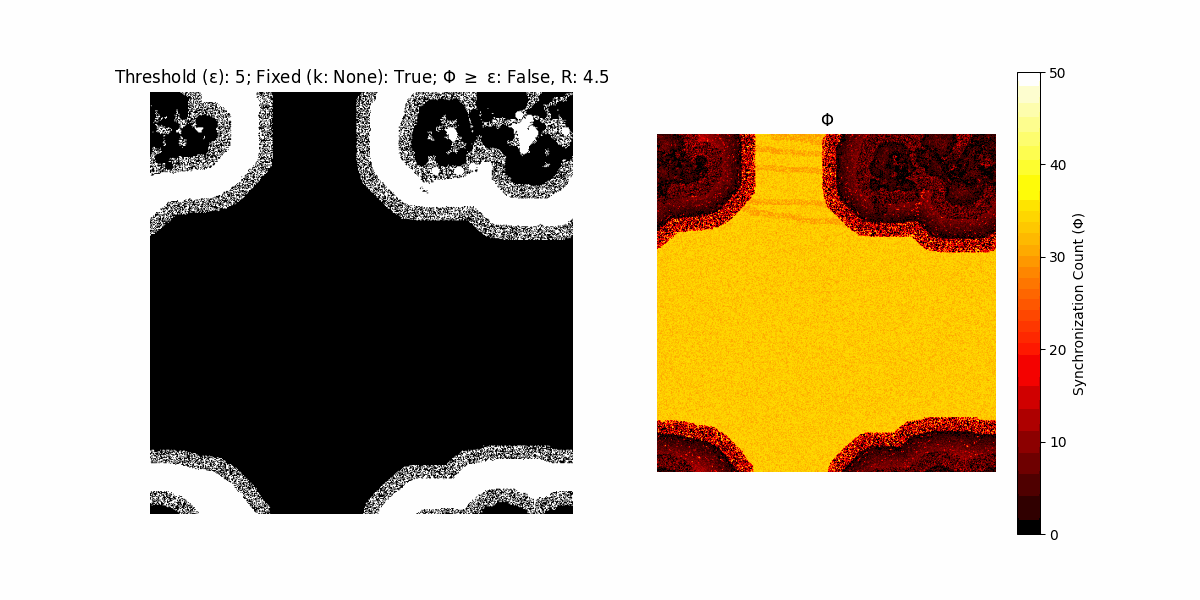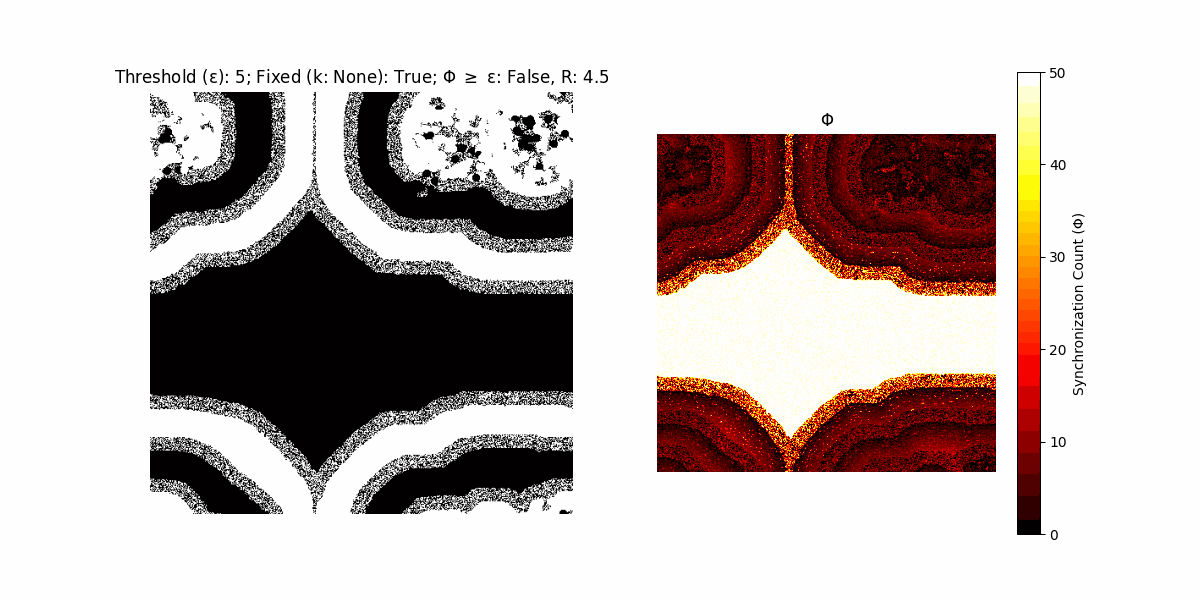
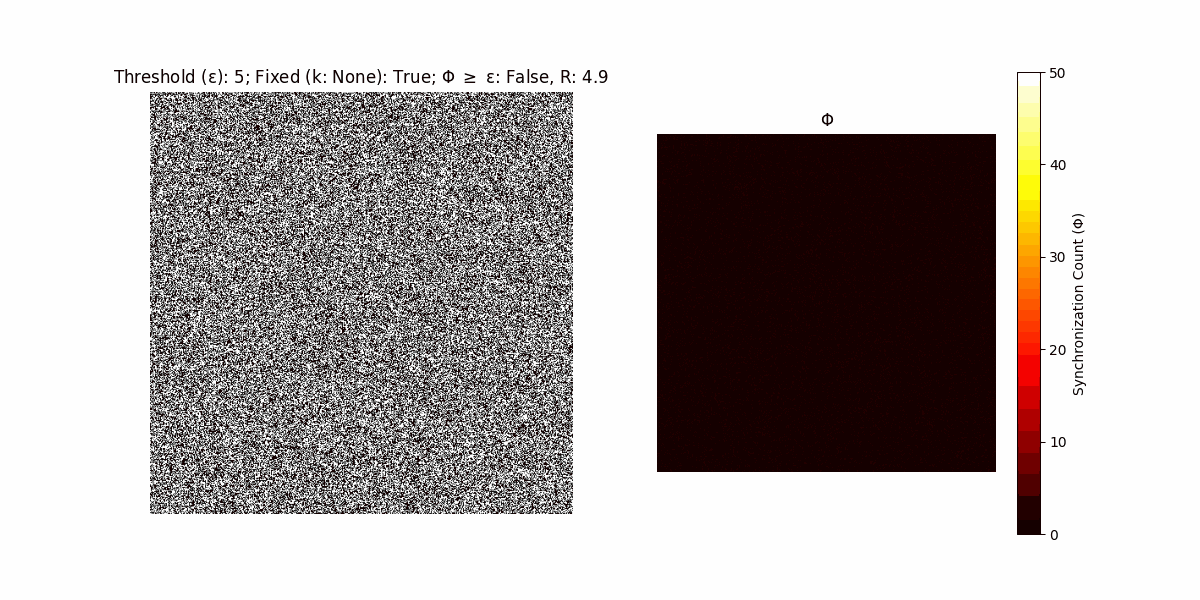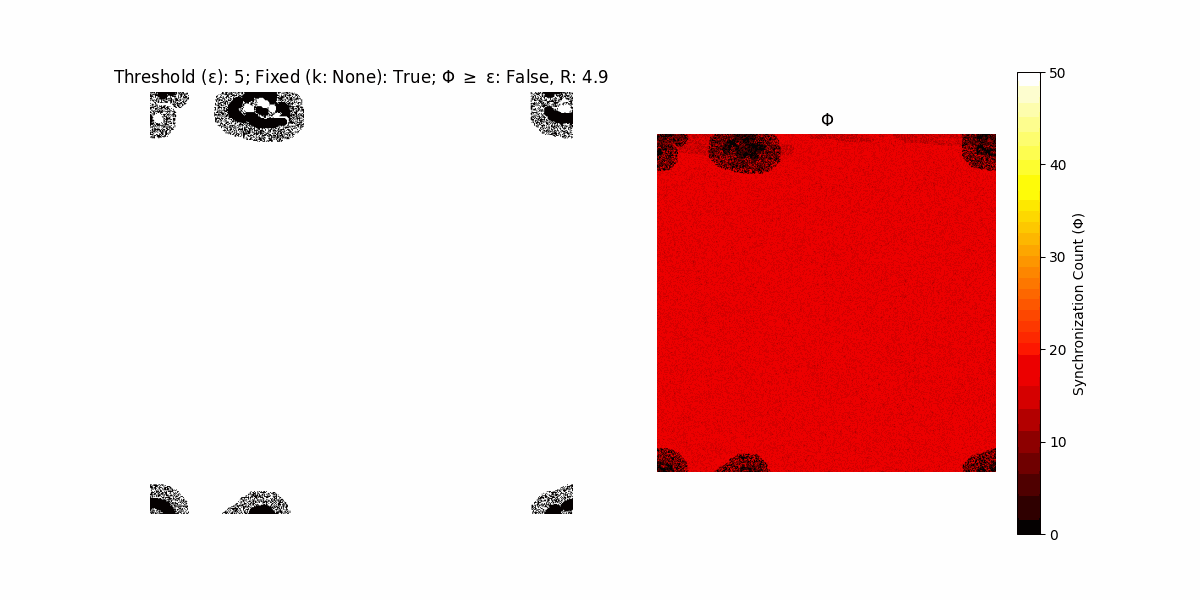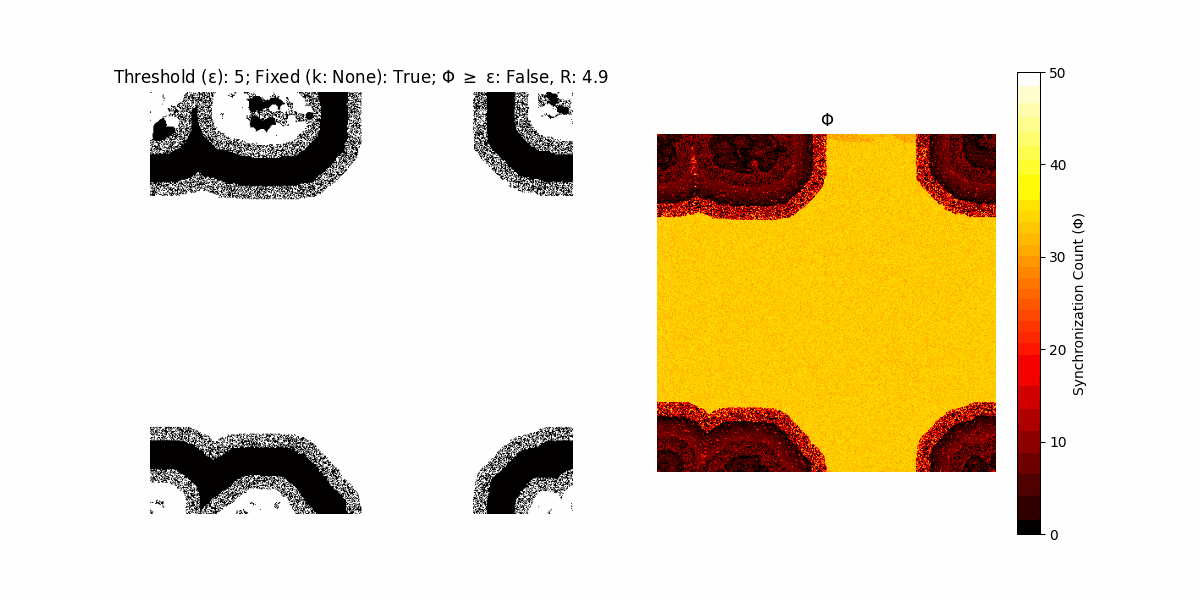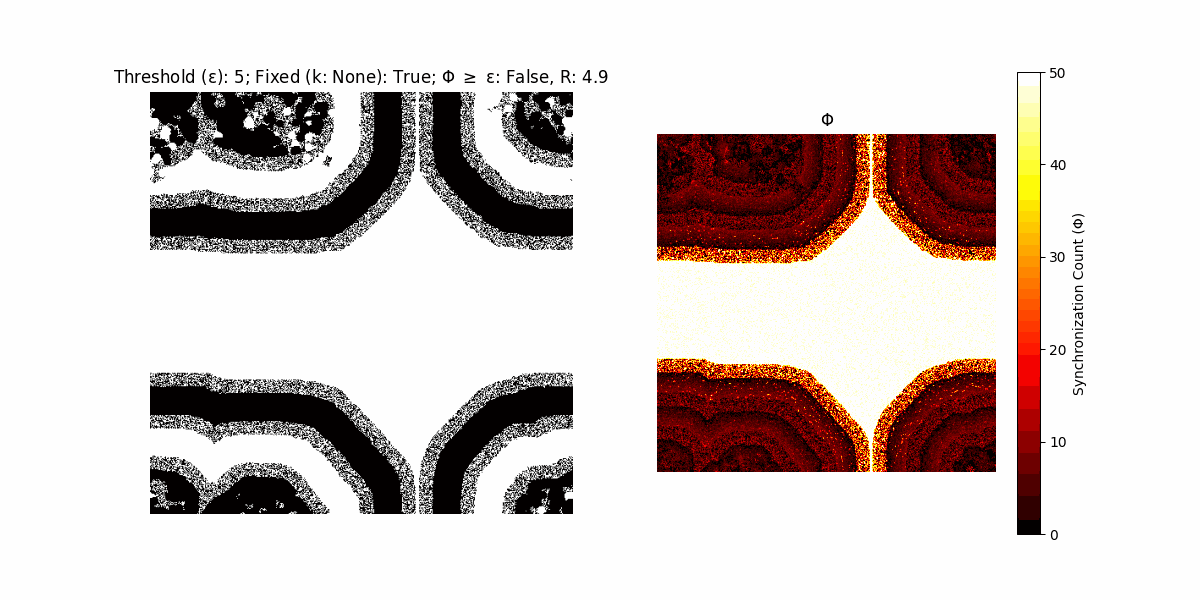
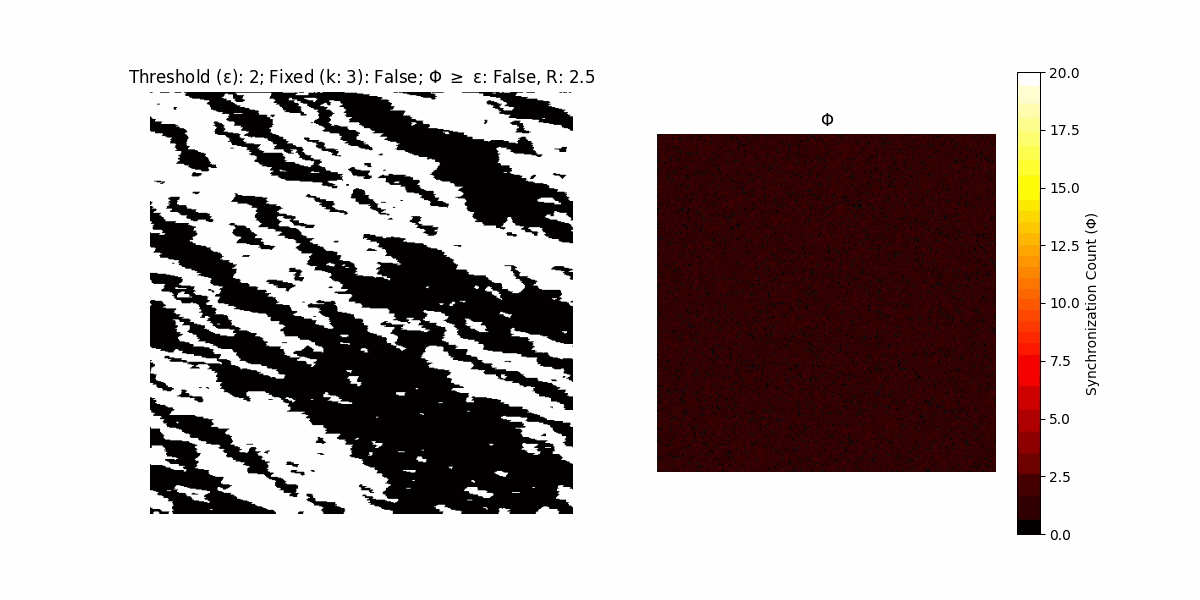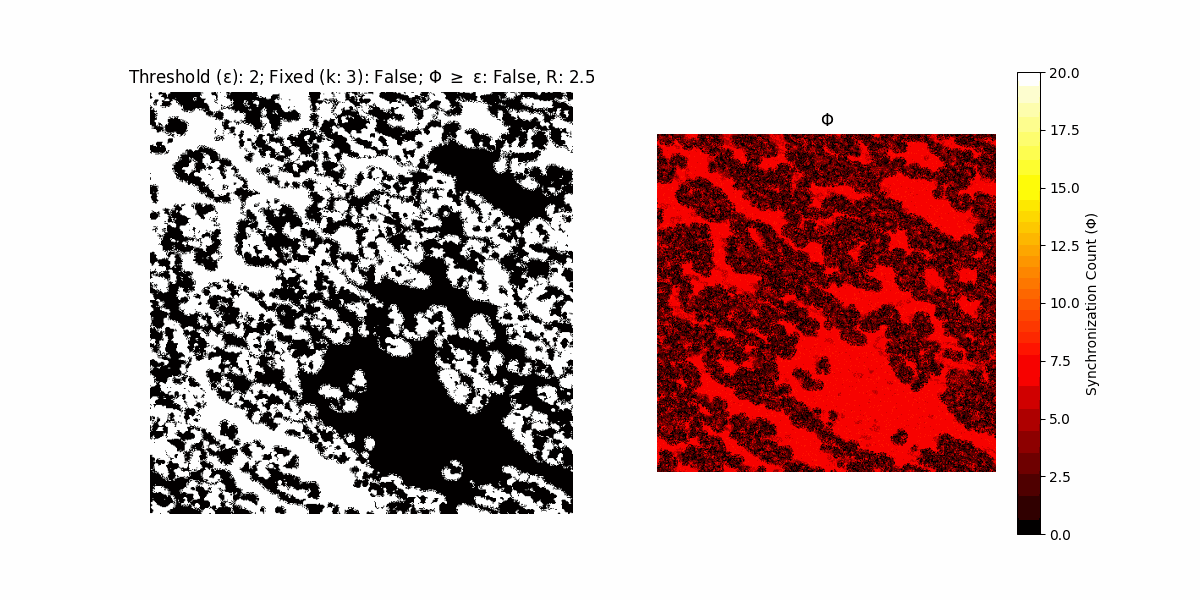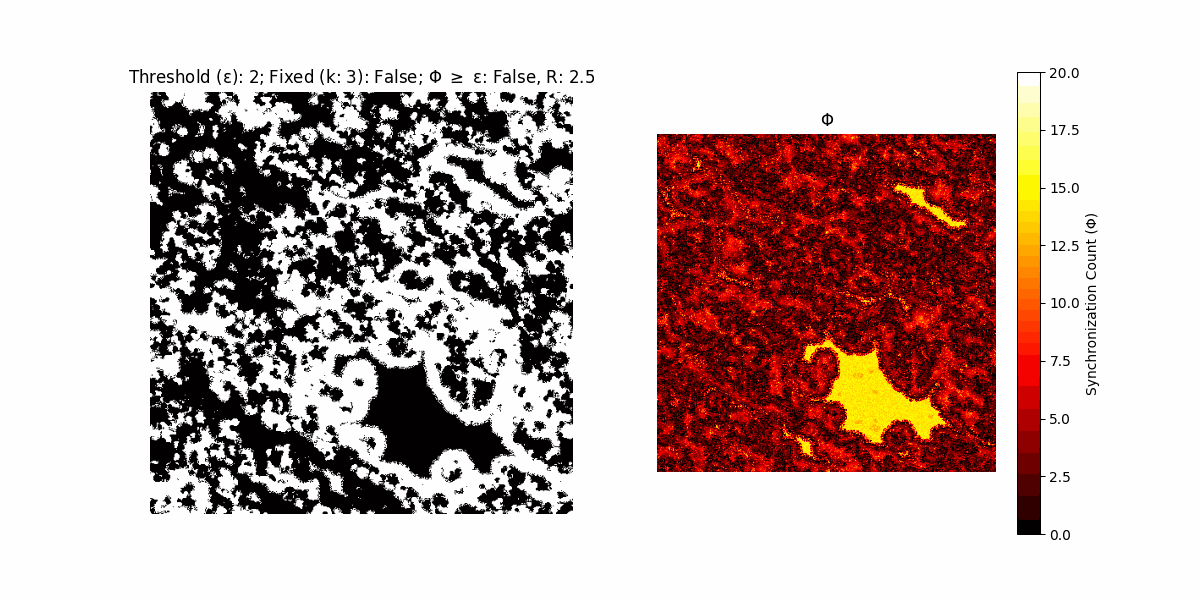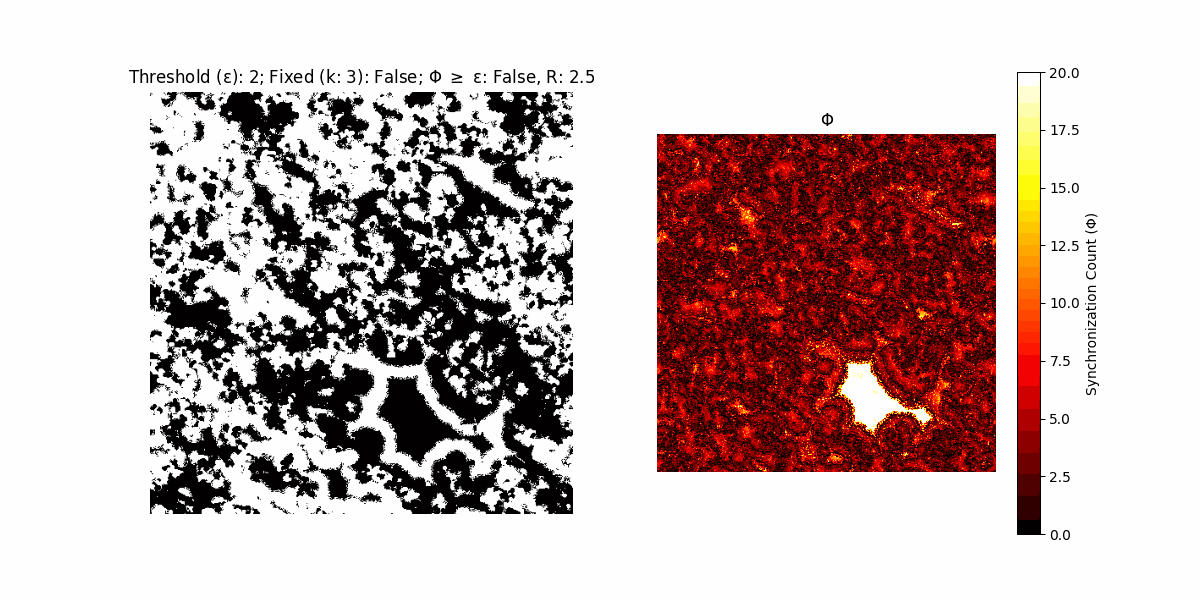
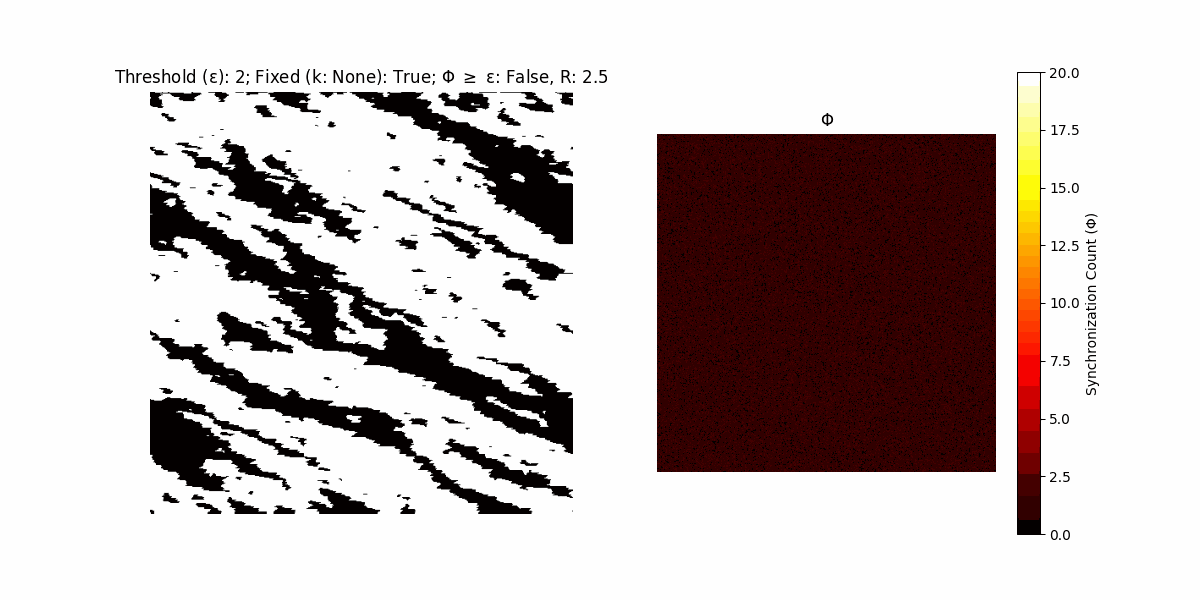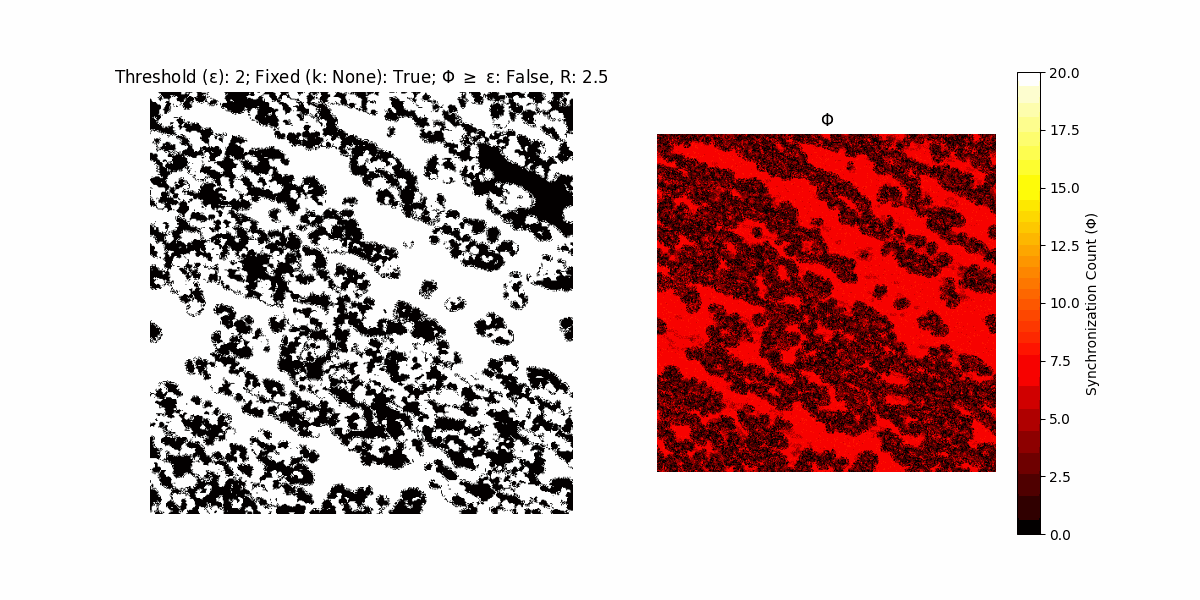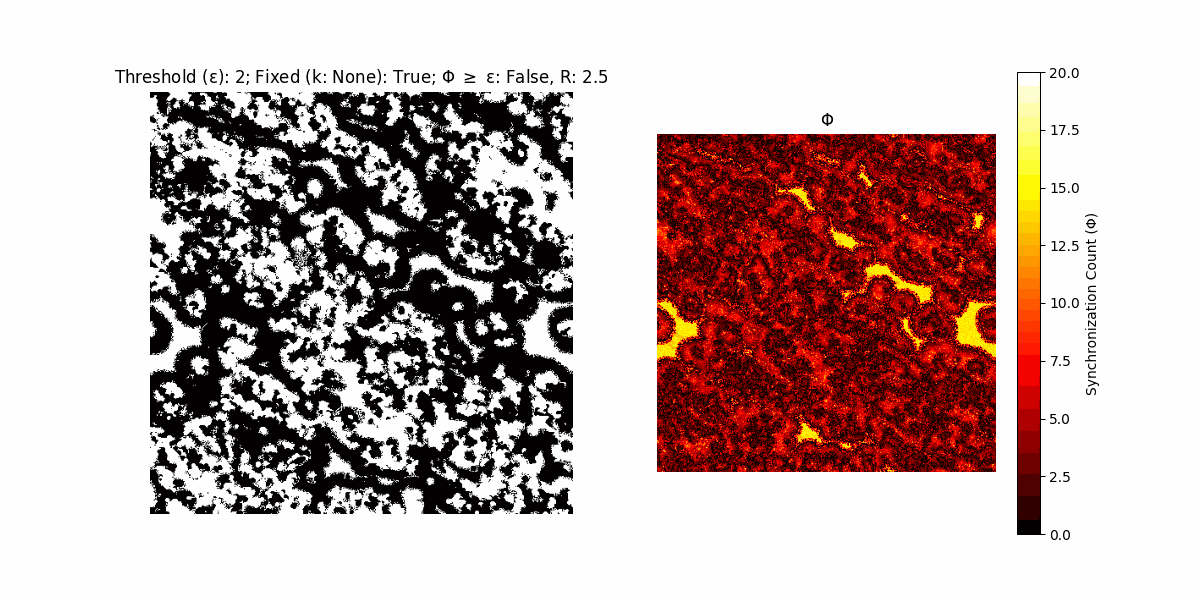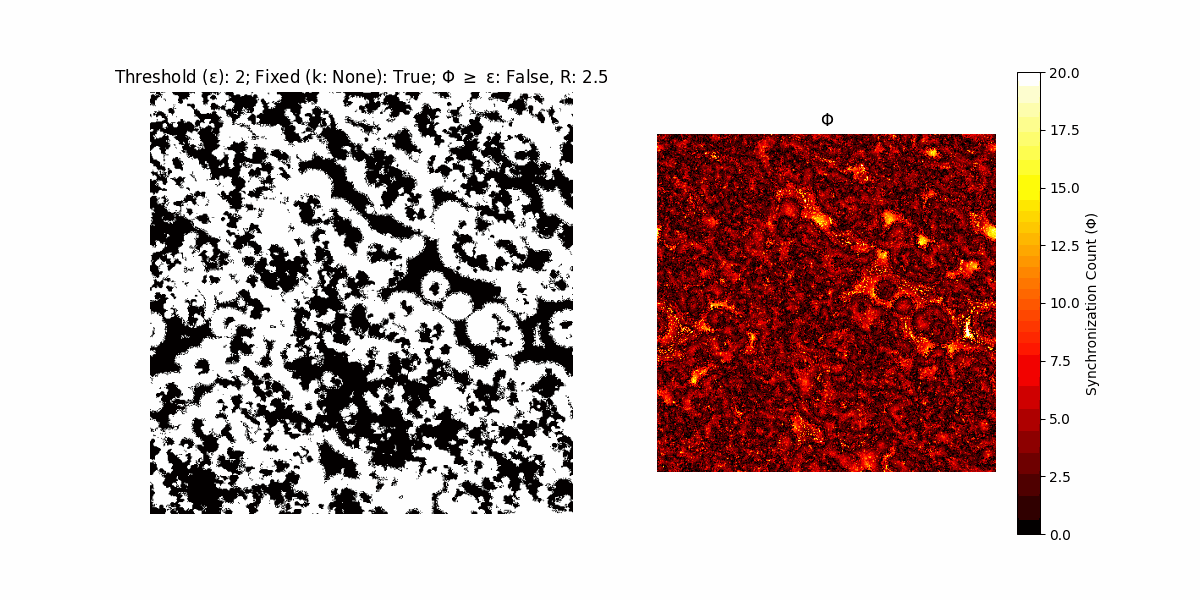
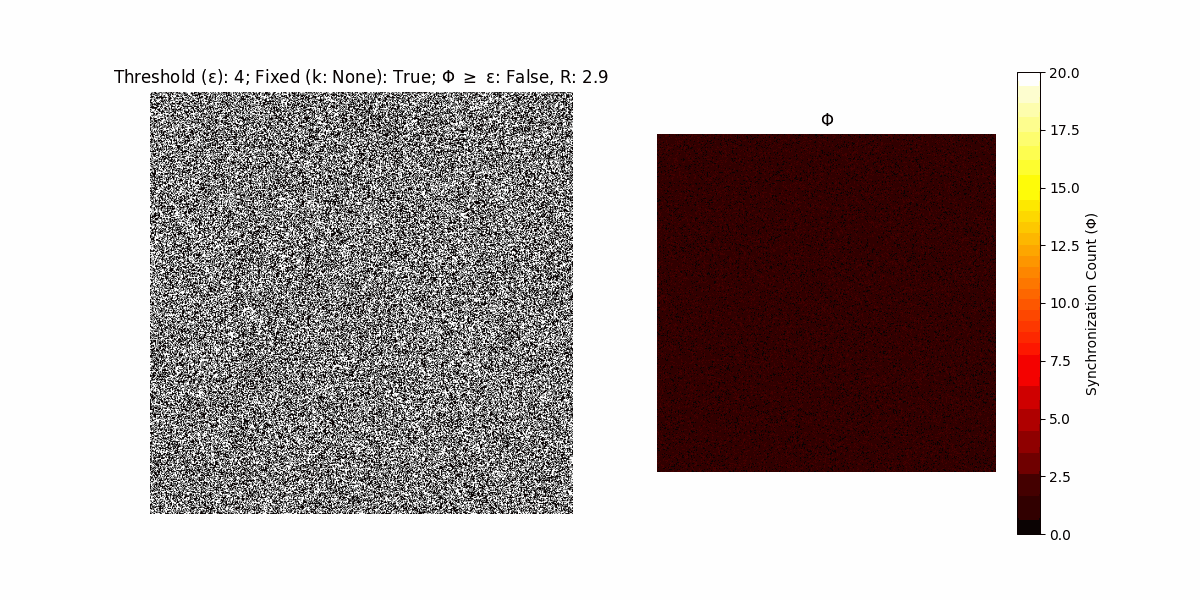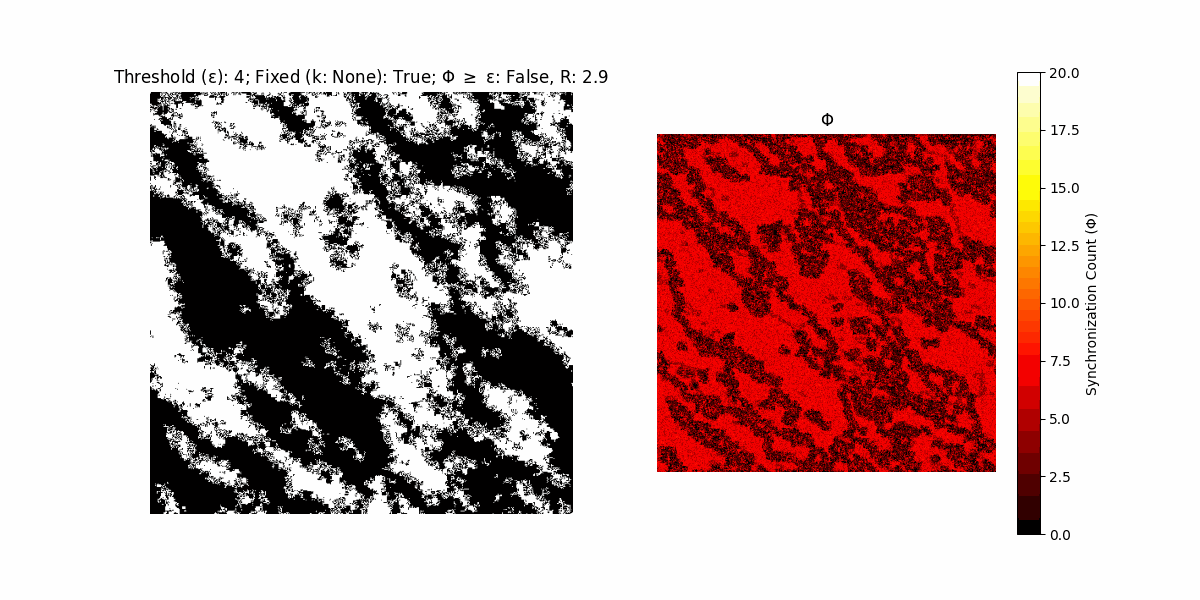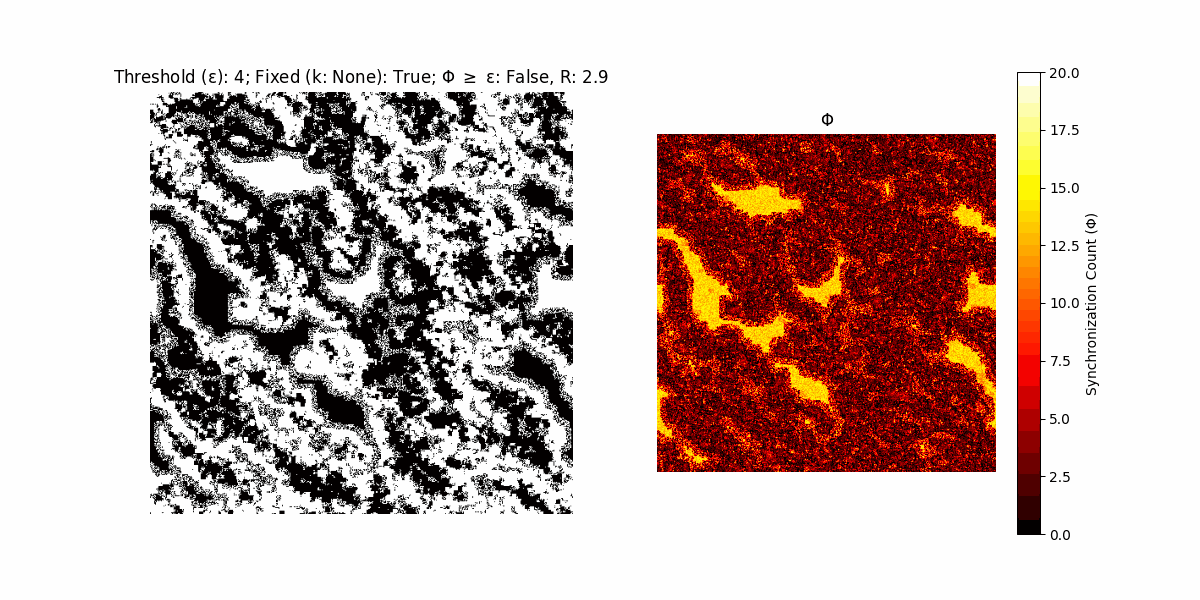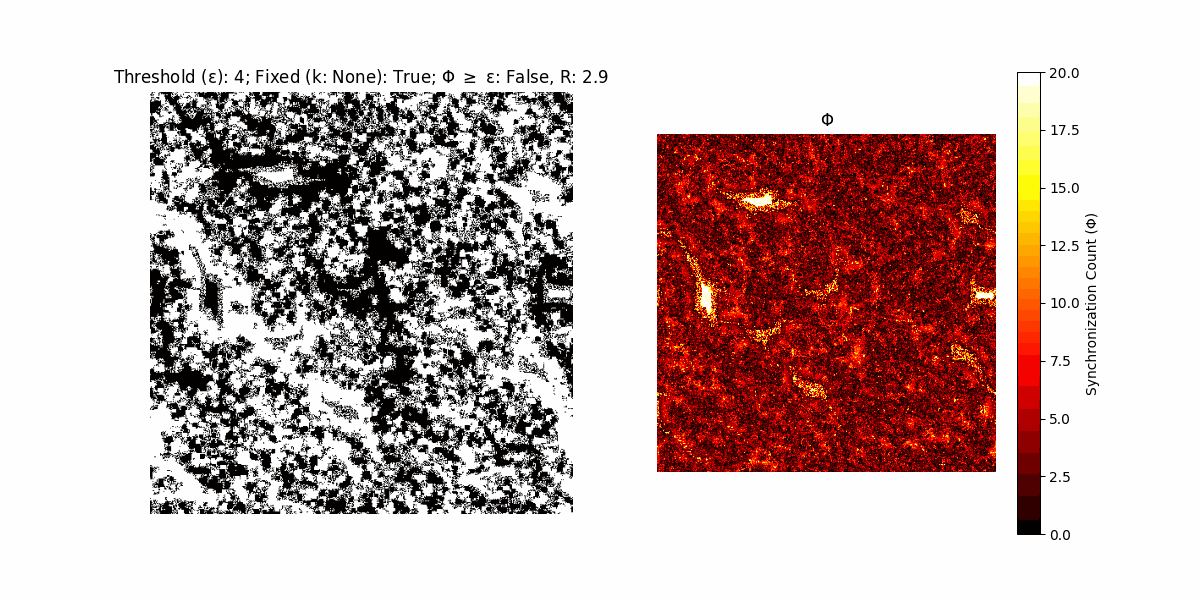
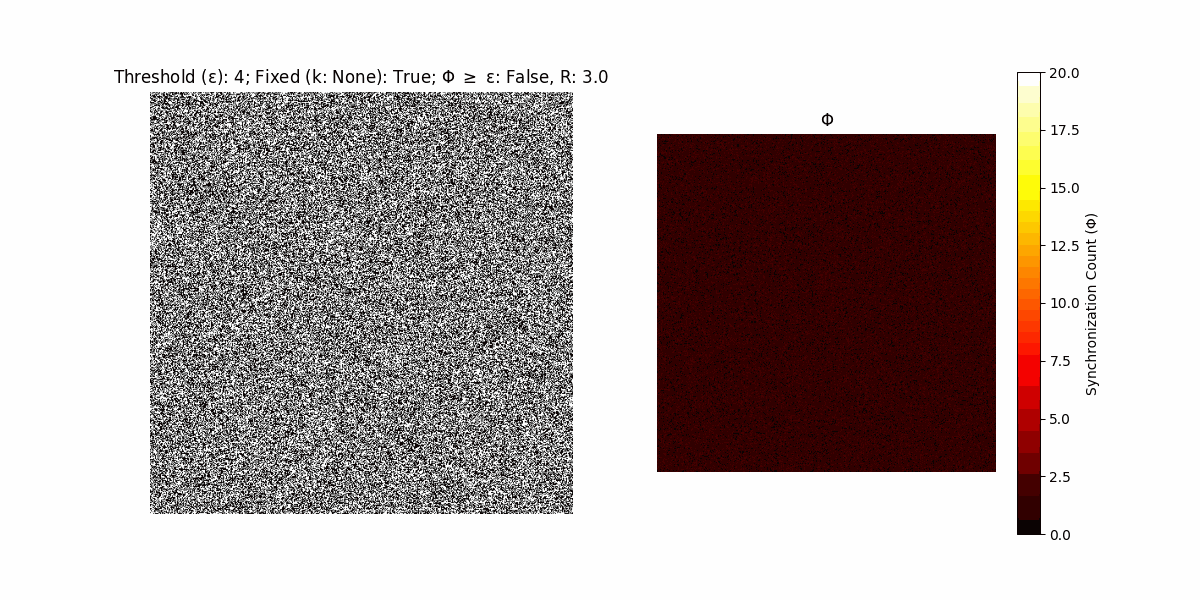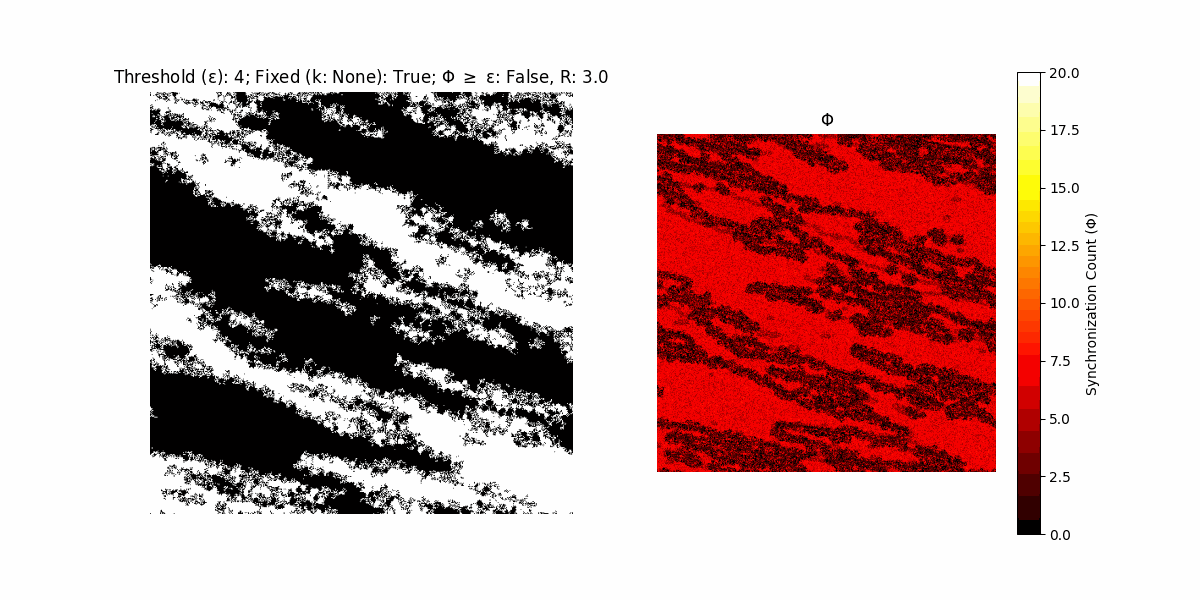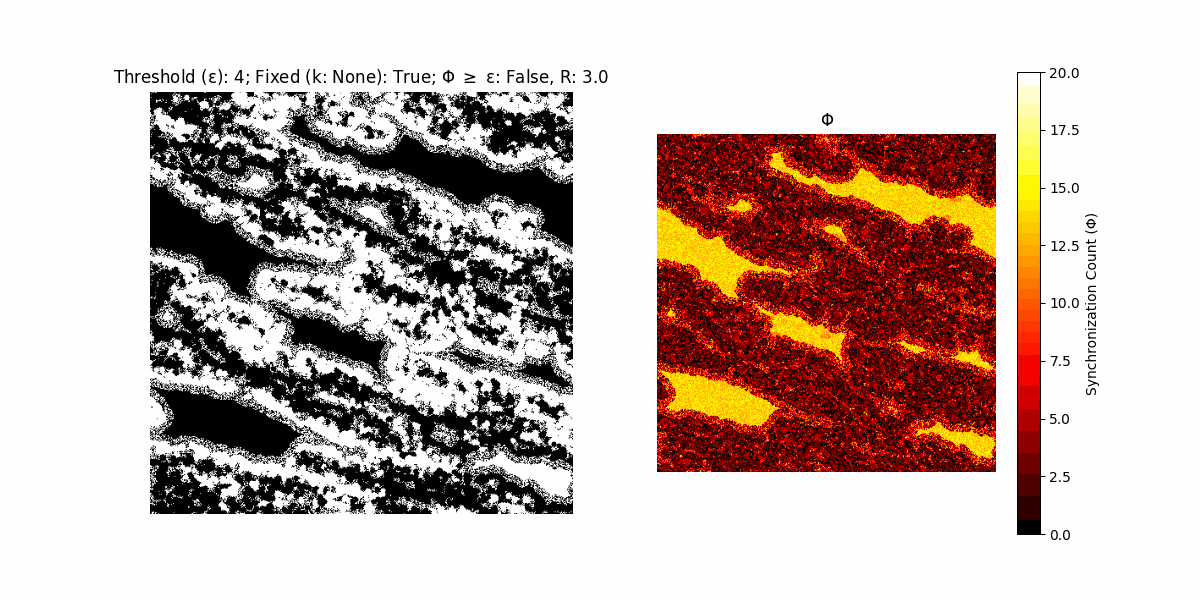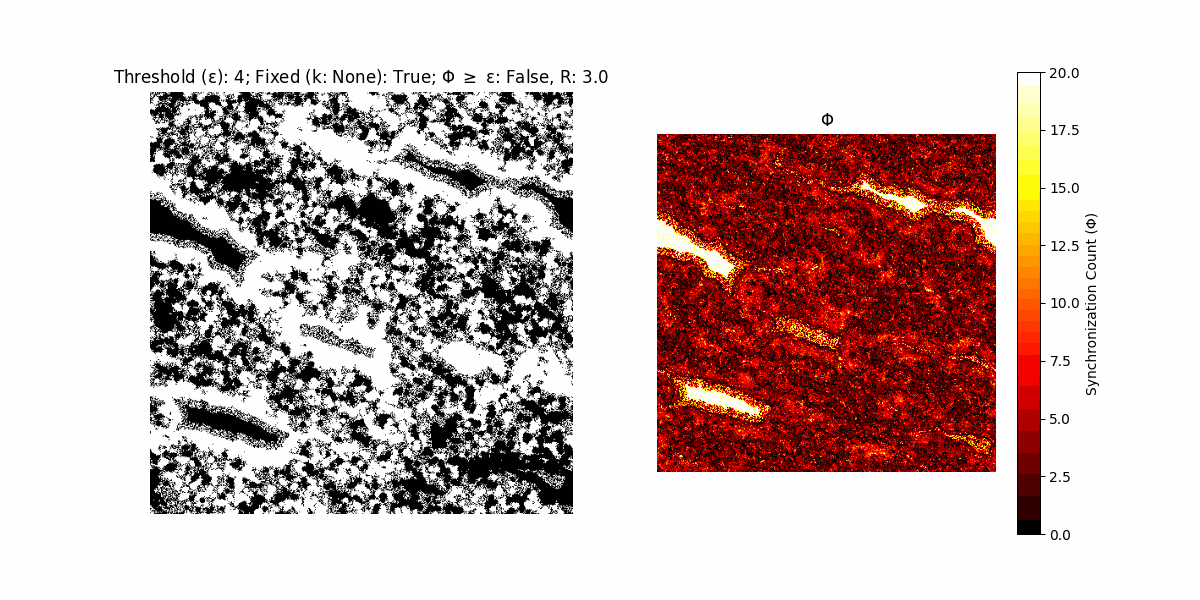
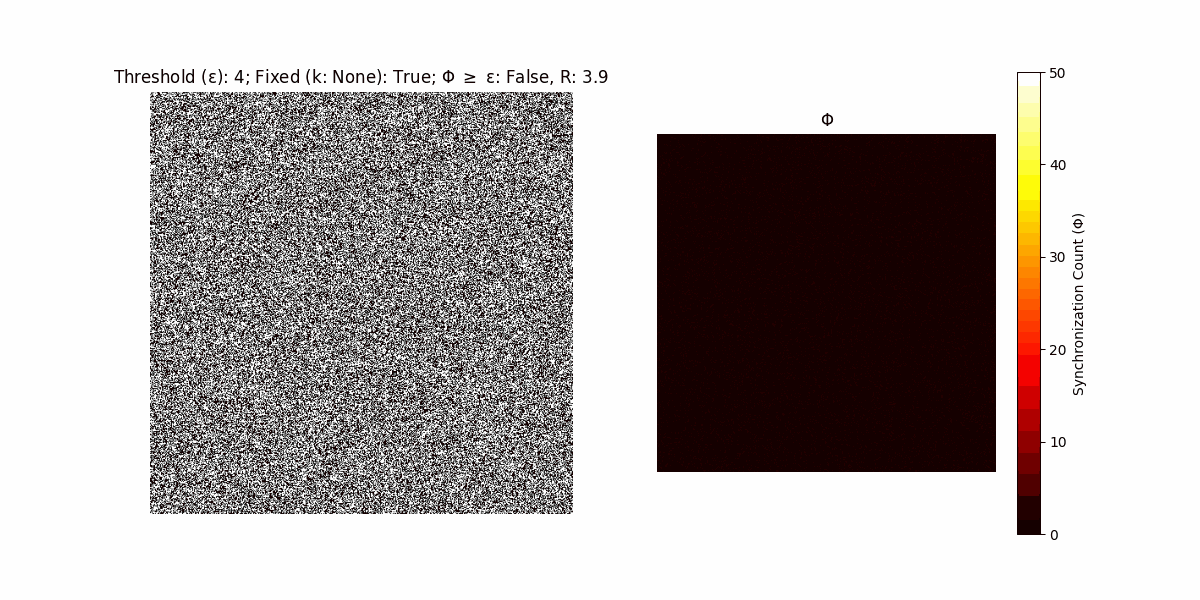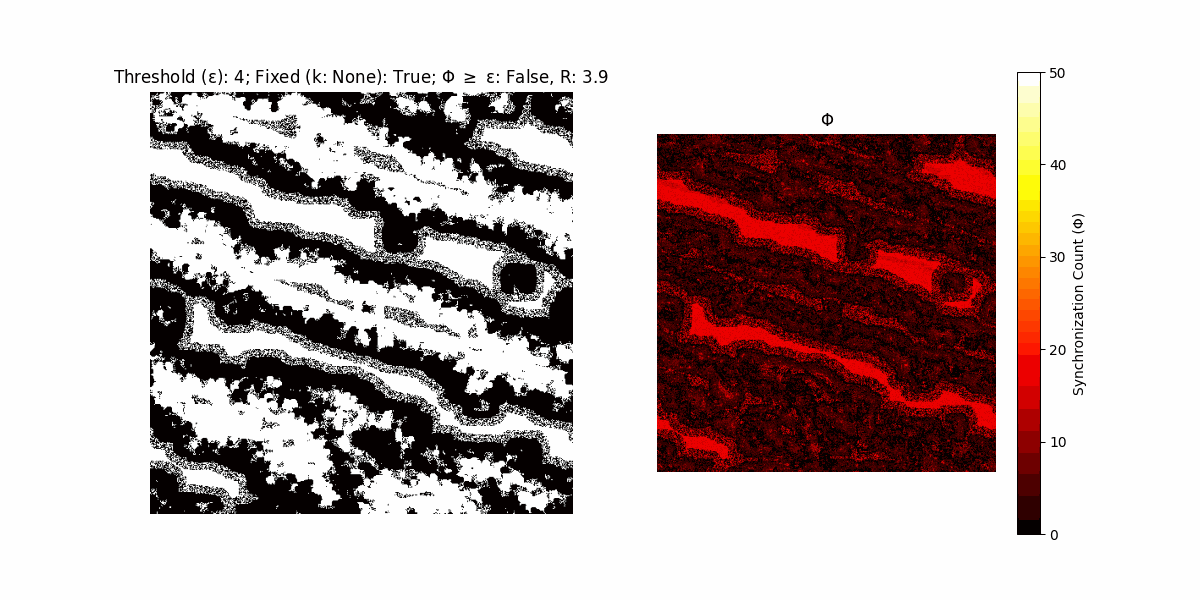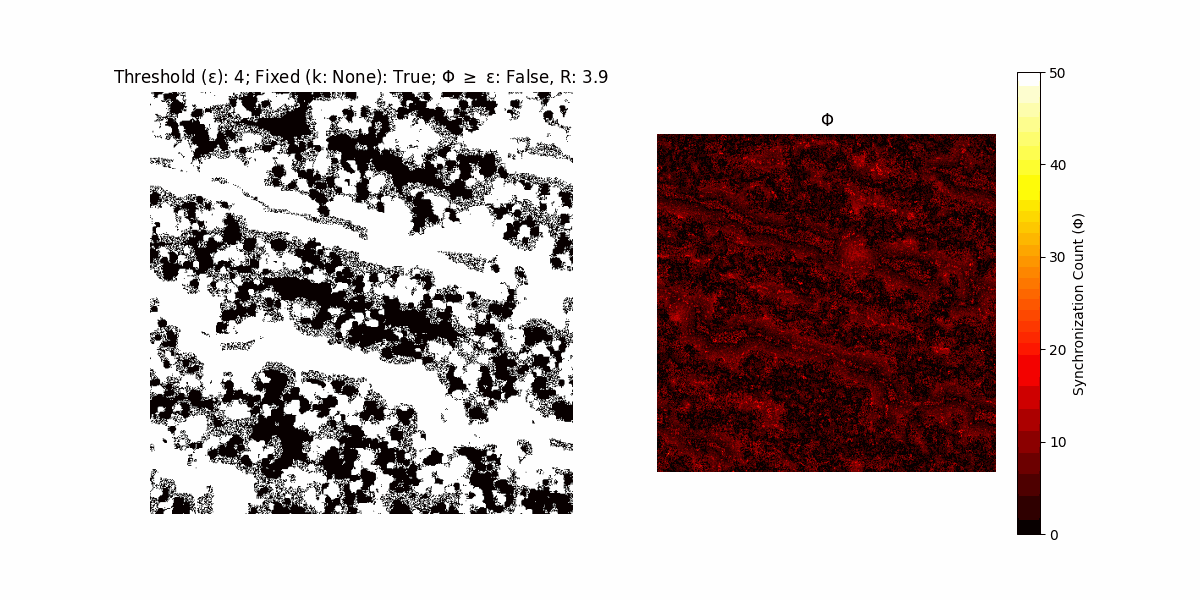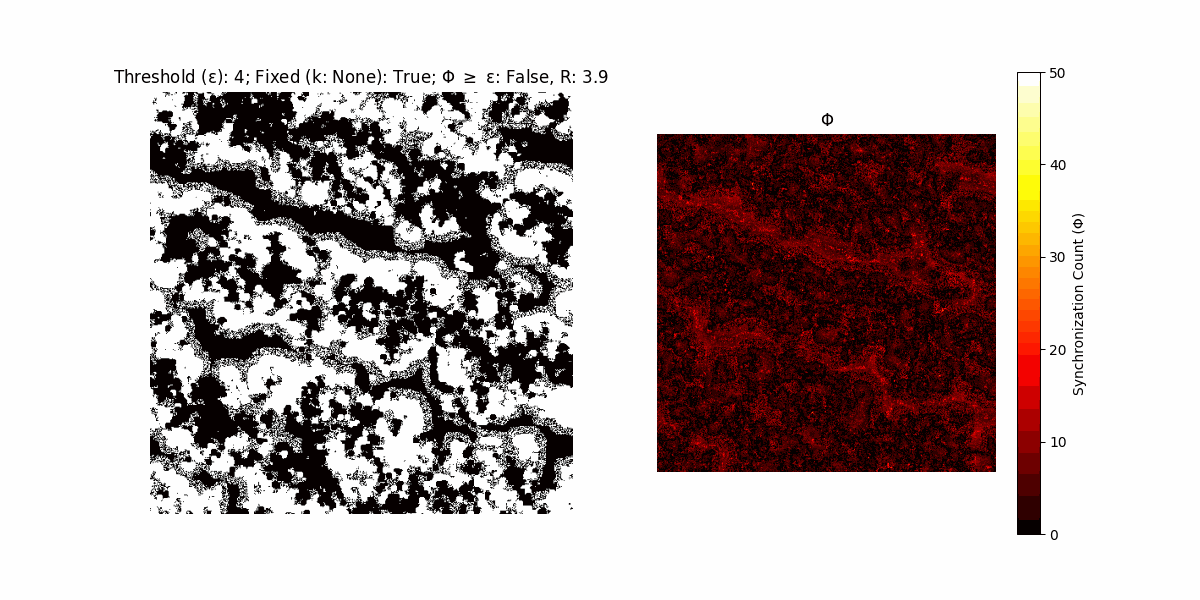
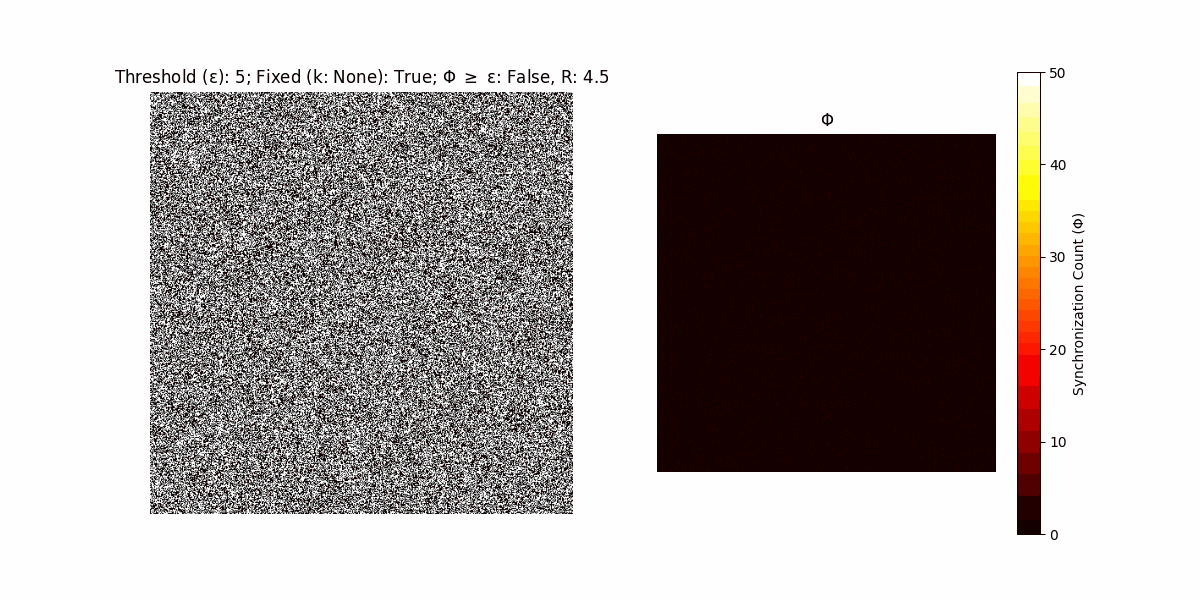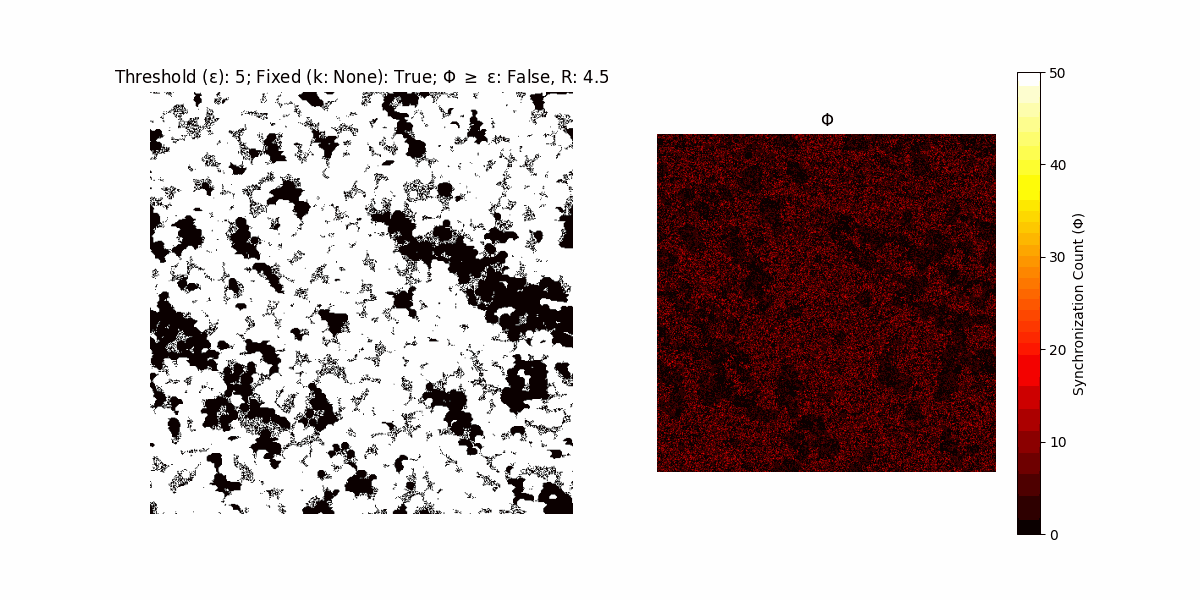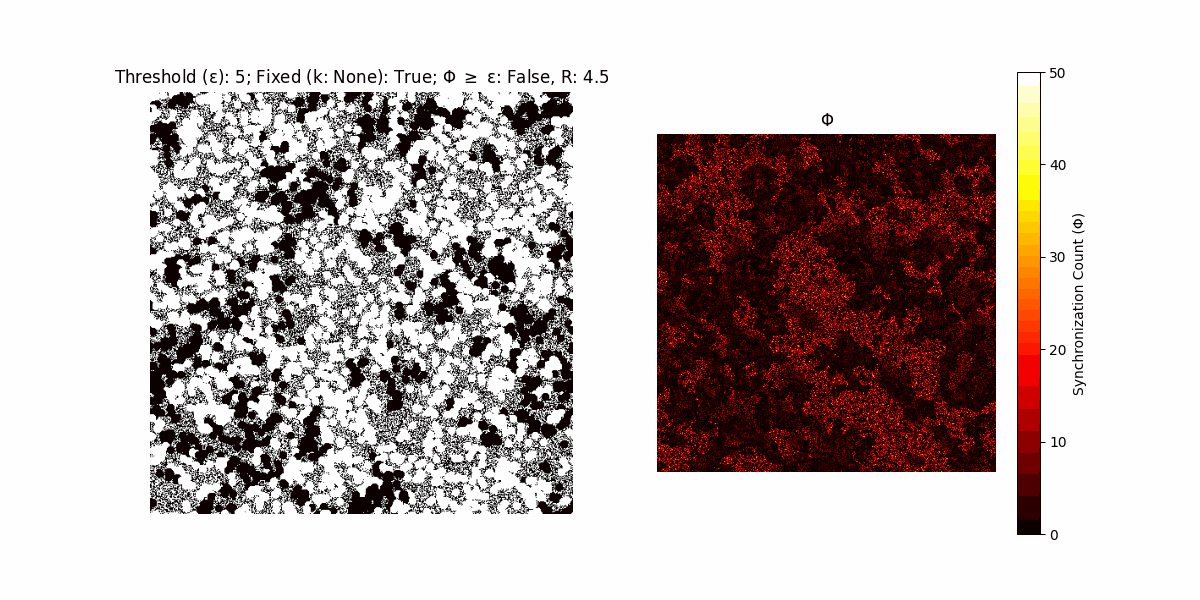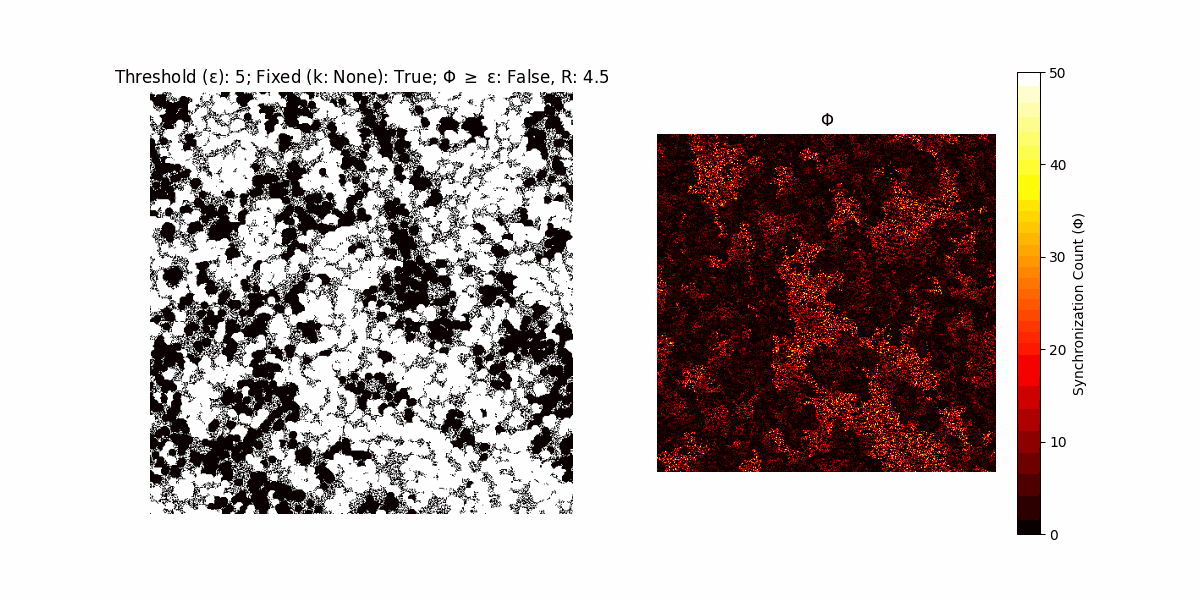
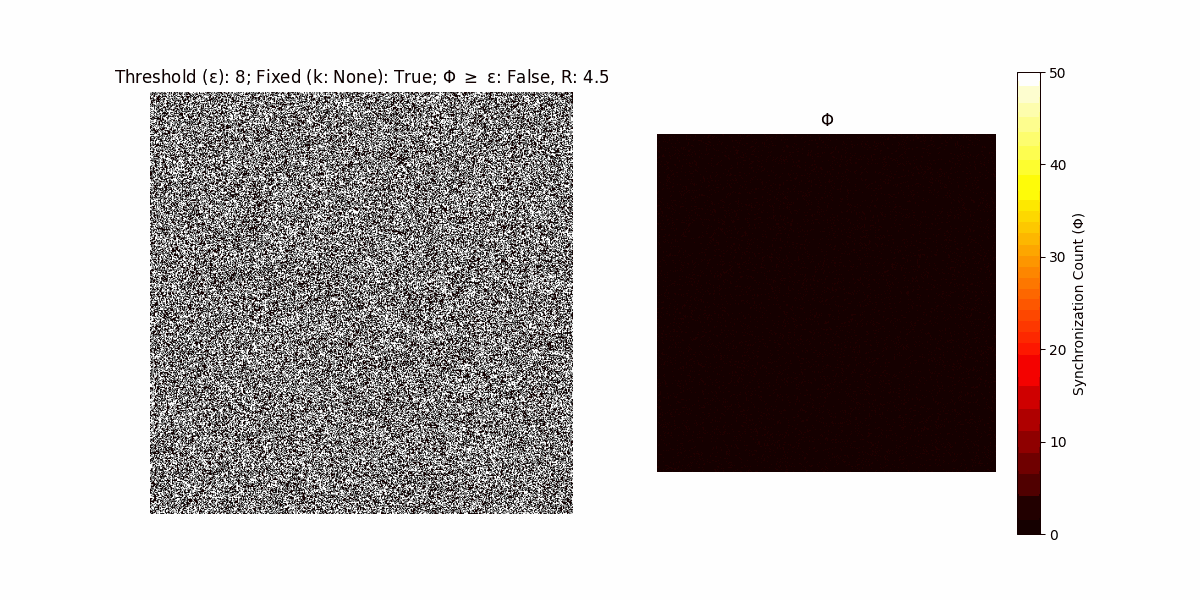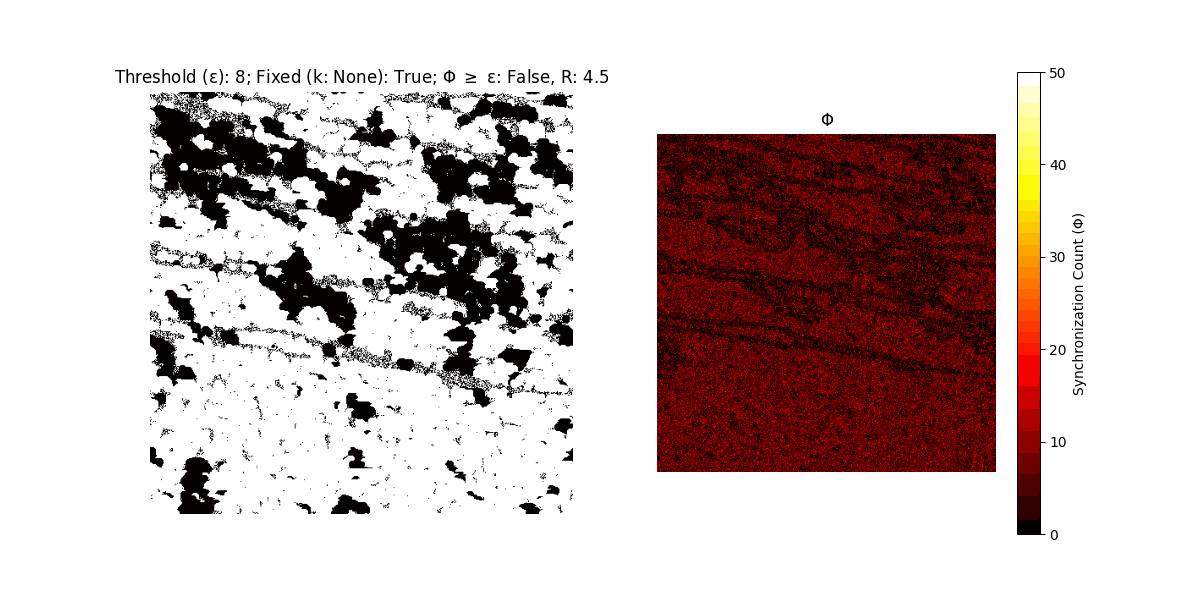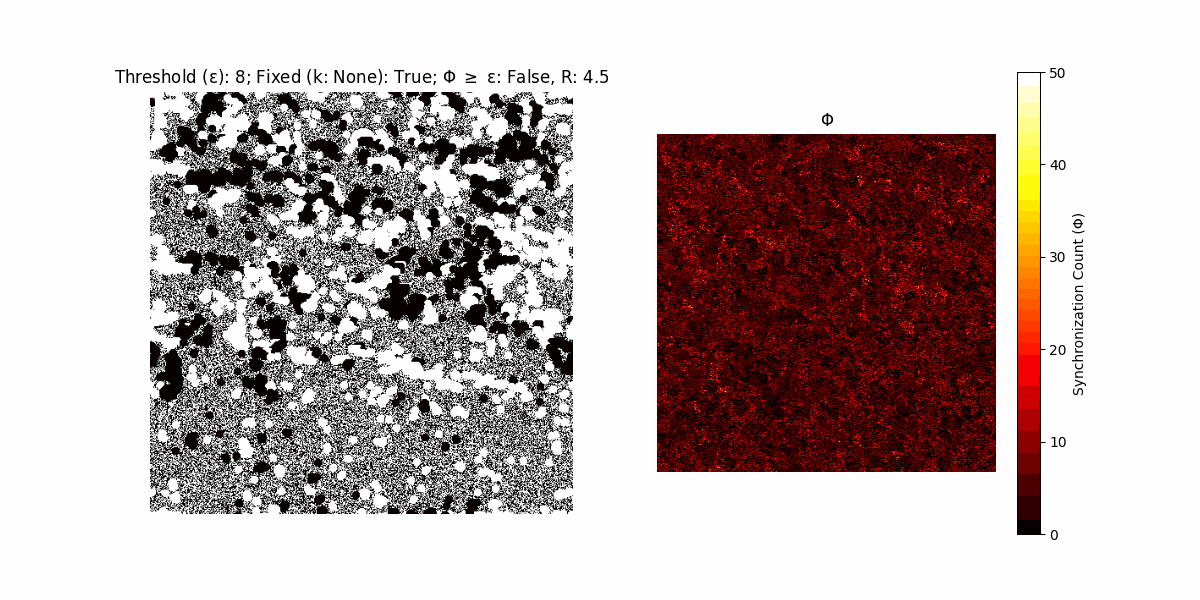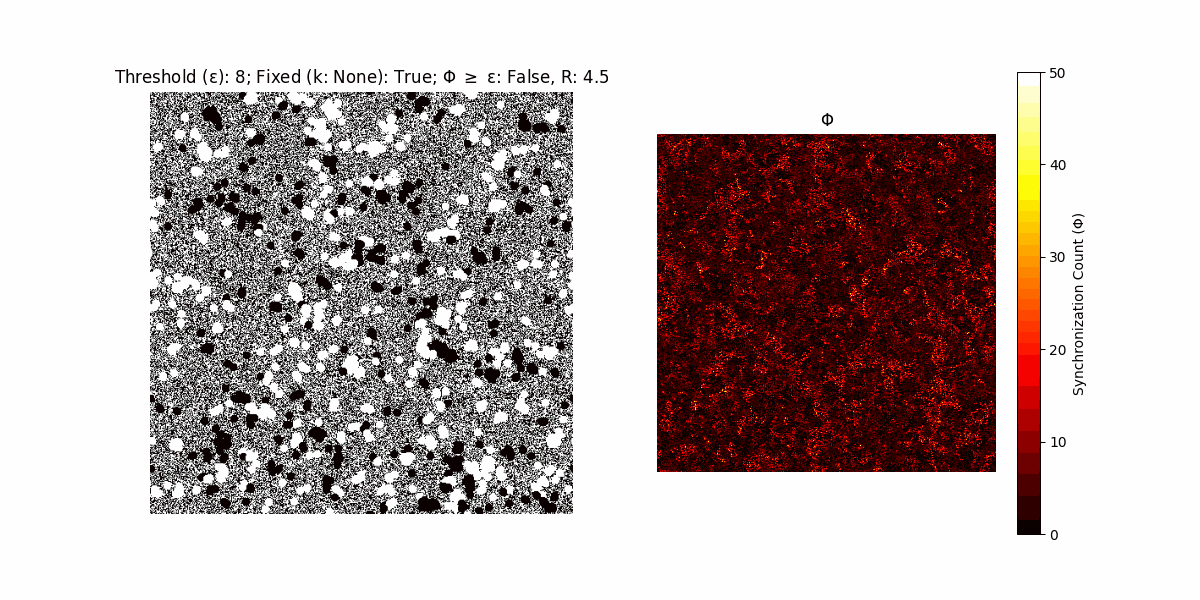
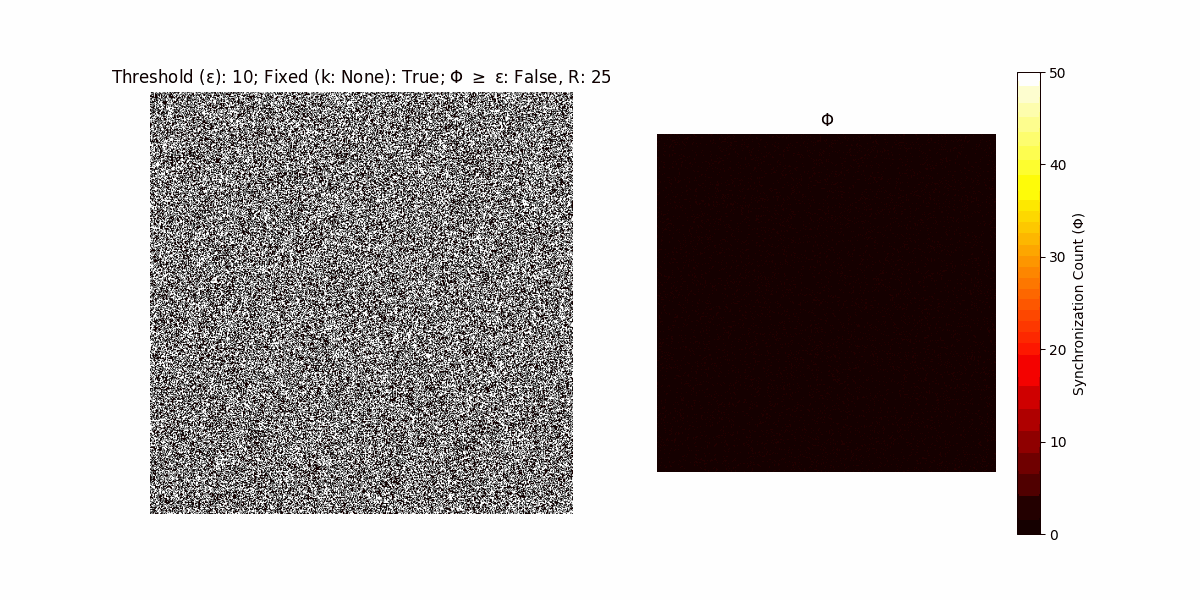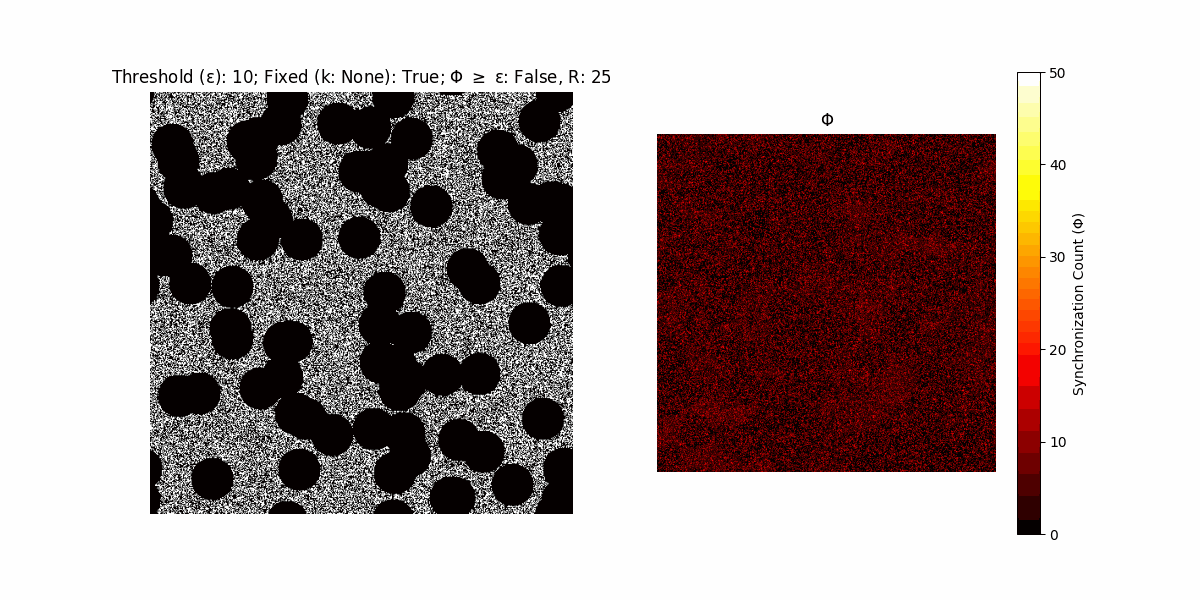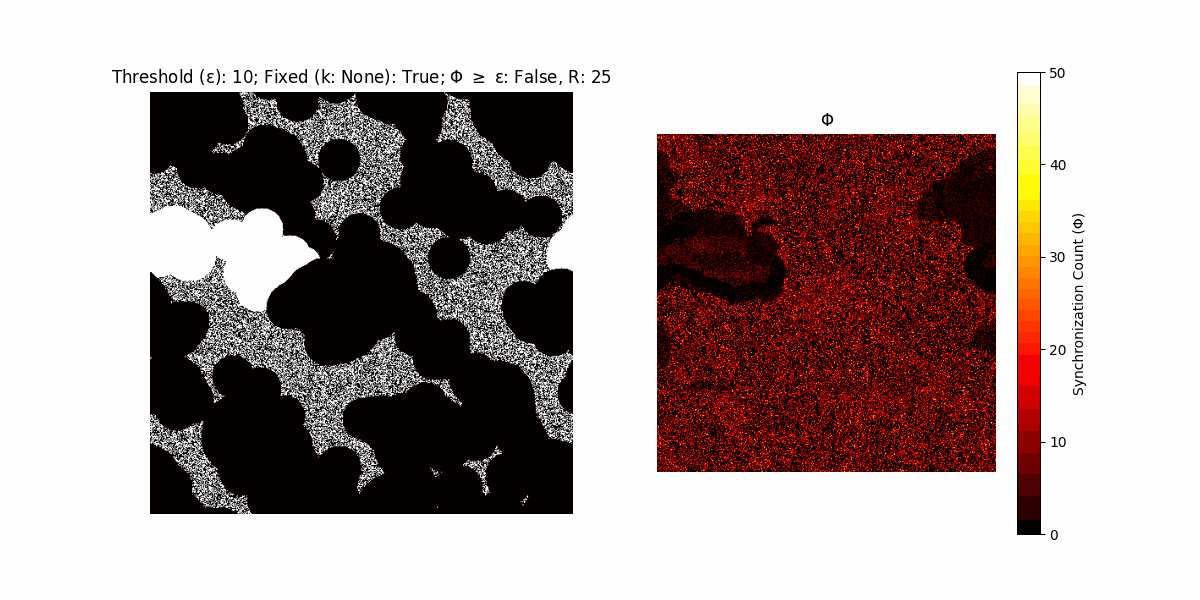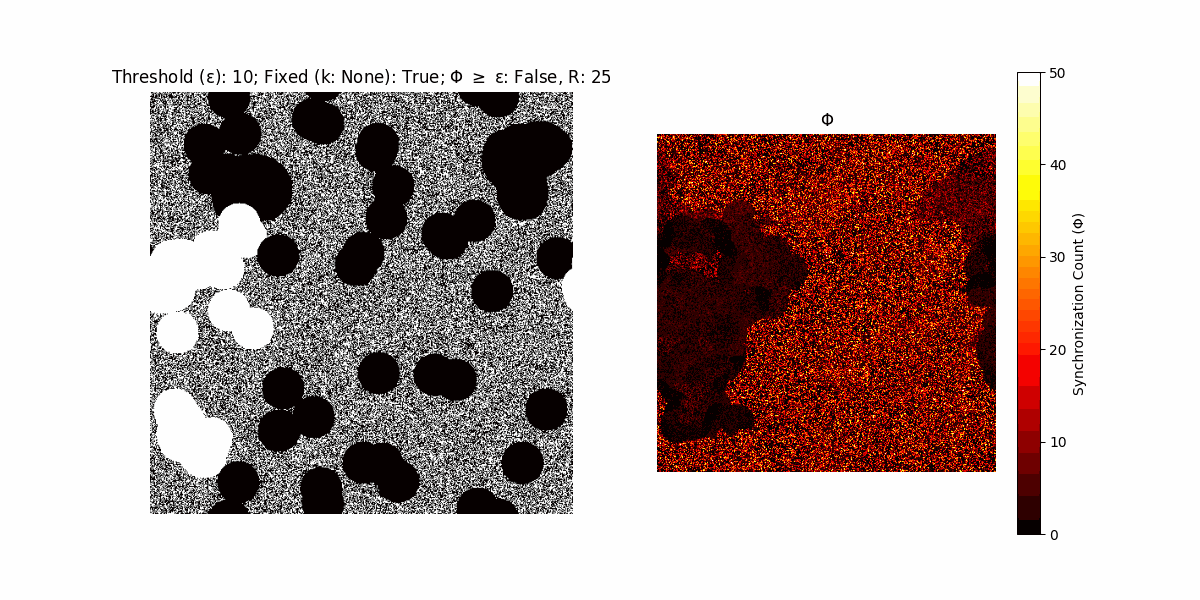
If a unit maintains its state after an iteration, regardless of its neighbors, its $\Phi$ value (which is supposed to mimick closure) increases by 1. Moreover, if the states respective to consecutive iterations are different, $\Phi$ is reset to 0. If $\Phi \geq \epsilon$, then the neighbors take the value of the main unit’s state, and an ensemble is formed. With regard to this, $\epsilon$ can be fixed (fix = True) or evolve over time (fix = False) with $ε = \textrm{int}\left(\frac{\textrm{iter}(1 - \textrm{H}(S))}{k}\right)$, where $\textrm{iter}$ is the number of iterations chosen, $\textrm{H}(S)$ the entropy of the net, and $k$ being an assigned integer. Additionally, there are two other options: geq_cond = True for $\Phi \geq \epsilon$ and geq_cond = False for $\Phi = \epsilon$.
There are multiple variants, such that main2.py generates the most interesting behaviour, it being applied with an euclidean neighborhood.
It is worth noting that the aim is to get behaviour increasingly closer to being characterized as autopoietic, and that these examples are far from such.
