Collatz's Ant and similarity of landscapes
This is a small development from the previous post, which is mostly focused on trying to understand where the similarities between landscapes come from (and what can be taken as proxies for these).
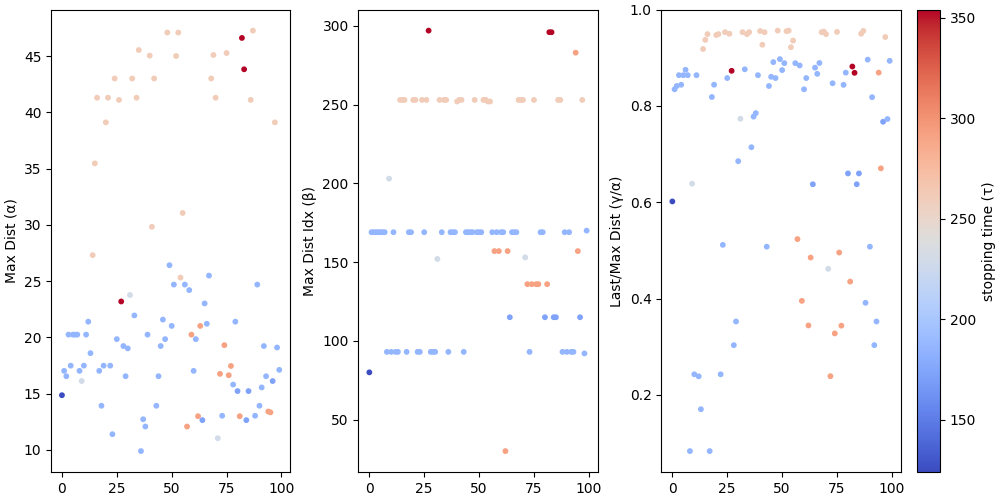
Considering the trajectories respective to the numbers from $n = 10^{20}$ to $n = 10^{20} + 100$, and the corresponding stopping times ($\tau$), maximum euclidean distance hit ($\alpha$) from the origin point $(0, 0)$ where the ant starts, the step at which such maximum distance is hit ($\beta$), and also the distance from the origin at the last step ($\gamma$) (in the third plot it’s normalized by $\alpha$), we have the following:
along with the corresponding landscapes for each trajectory.

The question is: what makes a certain landscape specific? As already seen before in the previous post, the answer isn’t the stopping time. In fact, there are vastly different landscapes with the same stopping time. One can also wonder if the maximum distance hit would give a clue. I have no intent of going about labelling each landscape according to which potential category it might belong to, so as to find if there are any discrepancies to be pointed at, but from a first look at such landscapes and also relying trivially on our intuition, we can of course state that $\alpha$ is always going to be minimally associated with different landscapes to the extent that these can be purely differentiated from each other given their dimensions. Beyond this, it’s not useful. In fact, if we think about scaling up the same pattern such that $\alpha$ increases, we’re more or less talking about the same landscape but with vastly different dimensions (such that there’s some type of scale-free similarity). Not that there are any examples of that in these trajectories, as that would also presumably only be noticeable when comparing trajectories with $\tau$’s with different orders of magnitude. But this suffices to make the point: $\alpha$ alone isn’t sufficient to make such discernment between landscapes.
One thing that’s easily noticeable from the start is that of $\beta$ or the step at which the maximum distance is reached. In fact, this provides some type of discreteness to our analysis. Despite very different maximum distances reached ($\alpha$), the step at which such $\alpha$ is reached seems to allow for grouping onto different categories. Or at least, this seems to be the case at a first sight. We have cases where both $\tau$ and $\beta$ coincide, as present in the following example:

Cases where there’s a slight discrepancy in $\beta$, for instance:

And cases where this completely breaks, such that $\beta$ is vastly different, with respect to the same landscape:

But here of course we notice why this breaks. There’s a slight number of steps at the start of the ant’s trajectory which pushes the formation of the landscape away from the origin, such that the maximum distance reached is going to be at earlier steps (i.e. decrease in $\beta$). This was at least my intuition at first, but it doesn’t seem to make the most sense given that $\alpha$ is relative to the distances of that same trajectory. Not relative to others’! So the question still remains: why shouldn’t $\beta$ still be the same even if in the second example there would be an increase of $\alpha$? And if not, why?
This might require seeing how these landscape are forming…
Respectively (and highlighting $\beta$ with red):


we see that those steps in the start which push the landscape up, do end up influecing $\beta$, but only indirectly through changing which part of the landscape is going to be considered maximally distant from the origin. Ok, that’s interesting. But a big coincidence? Now even stranger is when two considerably different landscapes not only have the same $\tau$ but also end up having the same $\beta$, as is the case with the following example:
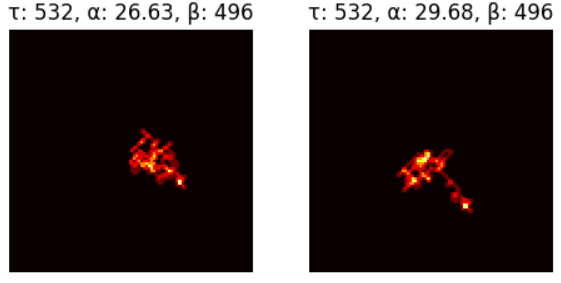
This is harder to explain. Perhaps there’s nothing to explain here. Perhaps a mere coincidence?
If we check the formation of the corresponding landscapes:


This is far from being the only example.
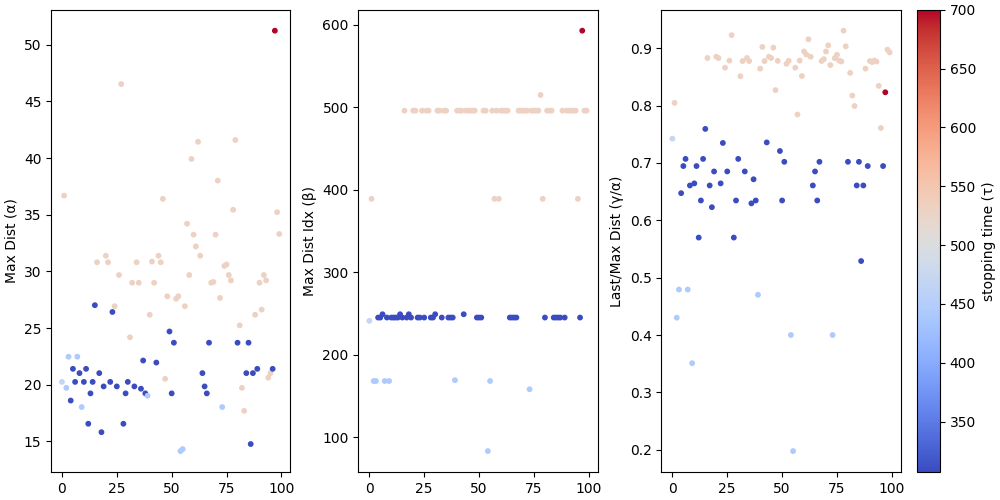
Examples from $n = 10^{10}$ to $n = 10^{10} + 100$, for which more of this can be verified.