Categorization of collatz numbers into 8 classes
Consider an empty tape with all unmarked cells, such that the reading head (standing initially in the middle of the tape) applies the collatz function to a starting $n$:
\[f(n) = \begin{cases} n/2 & \text{if} \quad n \equiv 0 \quad (\text{mod}\, 2) \\ 3n + 1 & \text{if} \quad n \equiv 1 \quad (\text{mod}\, 2) \\ \end{cases}\]flipping the state of the cell it currently stands in, and then moving left if $n$ is odd, and right if $n$ is even. It will do this until $n = 1$ is reached. Consider the example of $n = 27$:

and the corresponding tape development over time (↓):
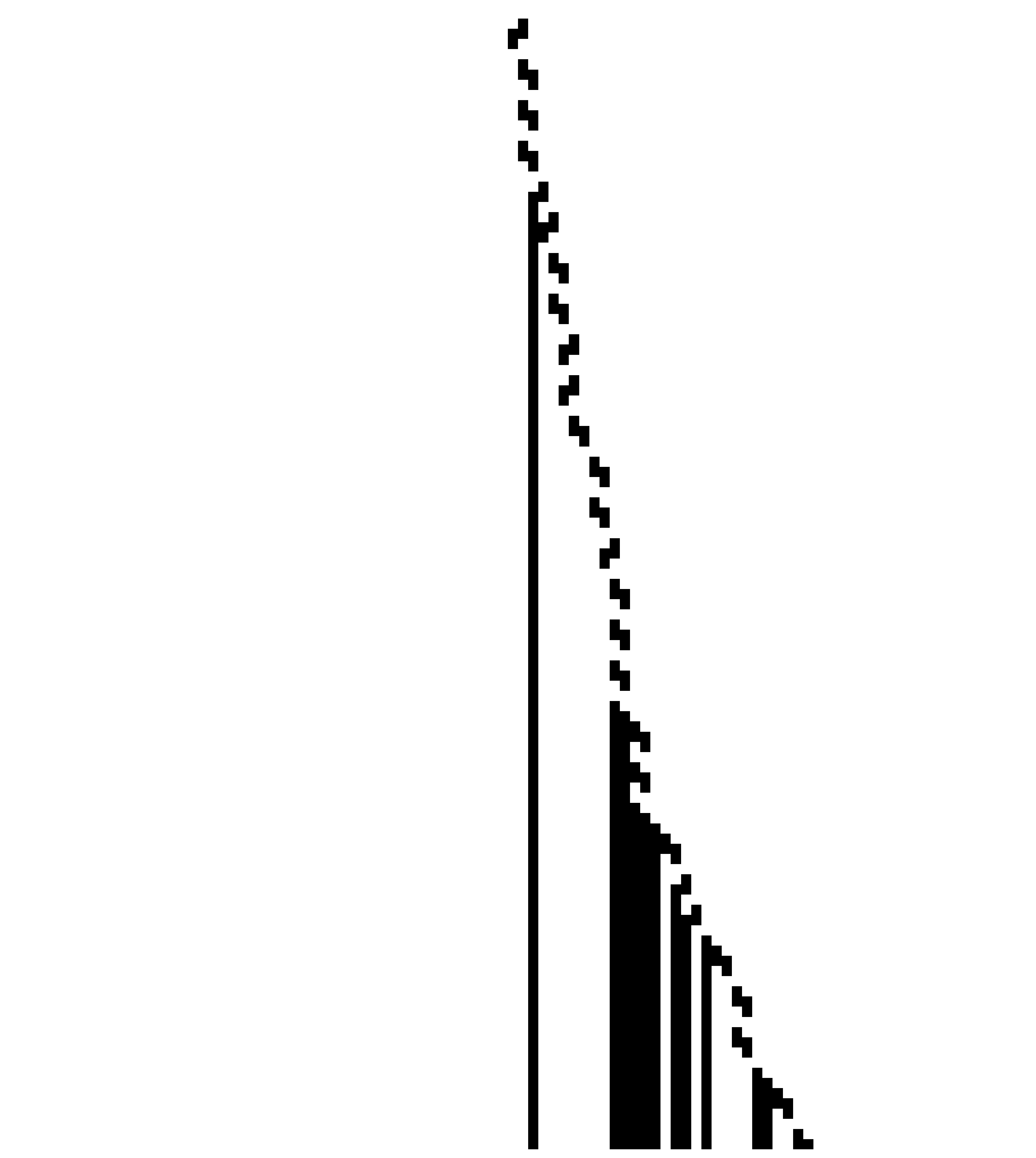
It has a stopping time of $τ = 111$, and at the last iteration before halting the tape has 13 marked cells (or 1s) - $Σ = 13$. Furthermore, from said last iteration we can also get the tape configuration in a compressed form (in a similar manner as discussed in this blog post). It will look like this $T = 1000000011111011010000110011$, which in a more compressed format will be shown as $T = 1^{1}0^{7}1^{5}0^{1}1^{2}0^{1}1^{1}0^{4}1^{2}0^{2}1^{2}$ (and of course ignoring the infinite sequences of zeros on the left- and right-hand sides of the tape, i.e. $T = 0^{\infty}1^{1}0^{7}1^{5}0^{1}1^{2}0^{1}1^{1}0^{4}1^{2}0^{2}1^{2}0^{\infty}$). We’ll also consider $1^{\text{space}(n)}$ where $\text{space}(n)$ is the number of uniquely visited tape cells. For $n = 27$, $\text{space}(n) = 30$, such that $1^{30} = 11111111111111111111111111111$. What we’re interested in is the ratio $\frac{T}{1^{\text{space}(n)}}$. In the case of $n = 27$ we have:
\[\frac{T}{1^{\text{space}(n)}} = \frac{1^{1}0^{7}1^{5}0^{1}1^{2}0^{1}1^{1}0^{4}1^{2}0^{2}1^{2}}{1^{30}} = \frac{1000000011111011010000110011}{11111111111111111111111111111} ≈ 0.009\]This ratio can generally be interpreted as the capacity of each $n$ to mark (and keep marked) every cell which it visits. The only examples with $\frac{T}{1^{\text{space}(n)}} = 1$ are powers of 2, which always move right and convert 0s into 1s until halting.
Ok. Now, let’s see how such ratio changes for $n$ from $n = 2$ to $n = 10^{3}$ (also representing a color-coding for $Σ/τ$ and showing a histogram for $T/1^{\text{space}(n)}$):

Ok, that’s somewhat interesting. Does such pattern change? Consider $n$ from $n = 2$ to $n = 10^{6}$:
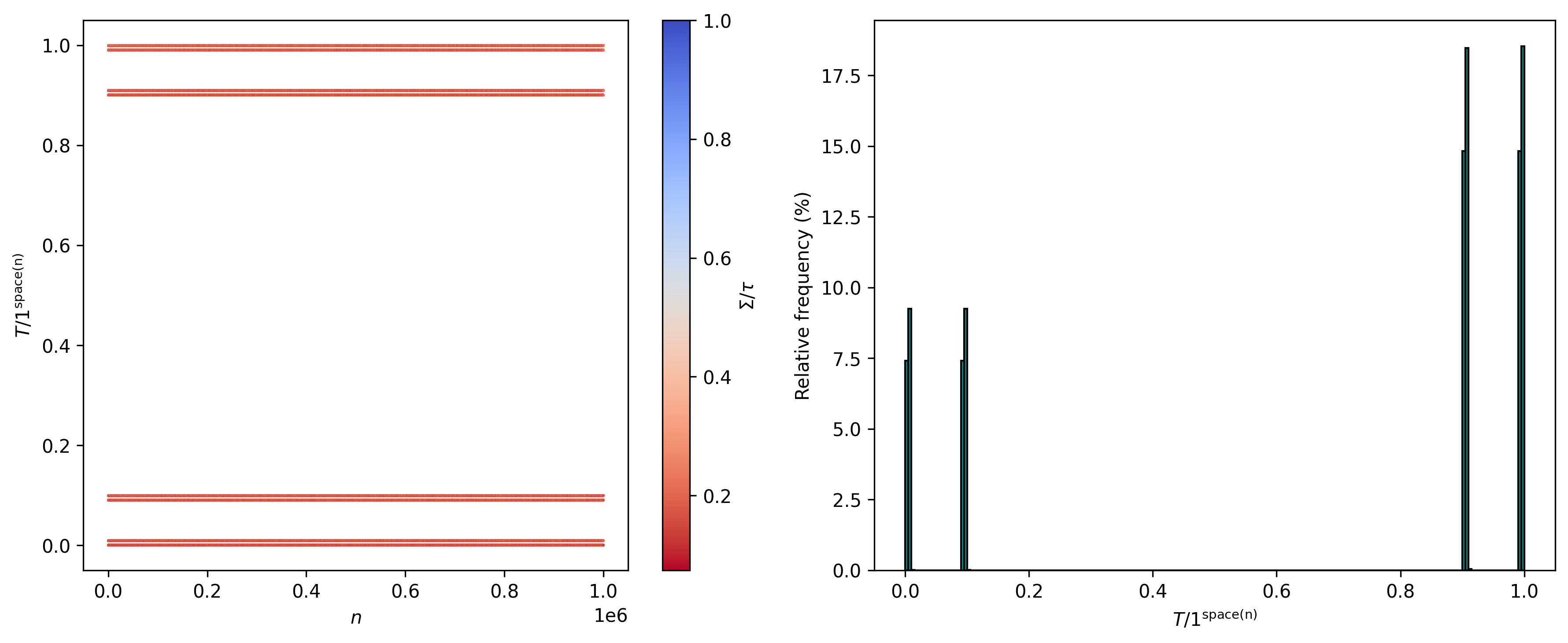
We still see those 4 major classes, each with 2 sub-classes. Additionally, and enumerating said (sub)classes in an ordered manner, we have convergence to the following relative frequencies (along with the thresholds of $T/1^{\text{space}(n)}$ for each (sub)class):
\[C_{1} ∈ [0, 0.005[\quad → \quad 7.4 \%\\ C_{2} ∈ [0.005, 0.01[\quad → \quad 9.25 \%\\ C_{3} ∈ [0.09, 0.095[\quad → \quad 7.4 \%\\ C_{4} ∈ [0.095, 0.1[\quad → \quad 9.25 \%\\ C_{5} ∈ [0.9, 0.905[\quad → \quad 14.8 \%\\ C_{6} ∈ [0.905, 0.91[\quad → \quad 18.5 \%\\ C_{7} ∈ [0.99, 0.995[\quad → \quad 14.8 \%\\ C_{8} ∈ [0.995, 1]\quad → \quad 18.5 \%\\\]Here we notice the relative frequencies for $C_{5}$ and $C_{7}$ being double those of $C_{1}$ and $C_{3}$, and likewise those of $C_{6}$ and $C_{8}$ being double those of $C_{2}$ and $C_{4}$. But why those specific frequencies? I would assume that a good chunk of this presumably has to do with the way the last iteration of the tape $T$ was represented (and correspondingly with $1^{\text{space}(n)}$).
But is there any reason a given $n$ should belong to anyone of these classes (beyond the trivially acessible explanation of its tape development)? In other words, can one find an expression for the numbers in any given class, thus being able to infer some part of the tape development merely by understanding which class a given $n$ belongs to?
Let’s restrict our examples to $n$ from $n = 2$ to $n = 100$. These are the corresponding $n$s distributed according to the class they belong to:
\[C_{1}: 11, 26, 47, 75, 90, 91\\ C_{2}: 10, 27, 42, 43, 46, 50, 58, 74, 78\\ C_{3}: 14, 34, 51, 62, 66, 79, 98\\ C_{4}: 3, 15, 18, 19, 35, 59, 63, 67, 82, 83, 99\\ C_{5}: 13, 20, 22, 45, 52, 57, 61, 77, 84, 92, 94, 100\\ C_{6}: 5, 21, 23, 25, 28, 29, 36, 37, 39, 53, 54, 55, 68, 69, 85, 86, 87, 89, 93, 95\\ C_{7}: 7, 17, 31, 33, 40, 44, 49, 56, 71, 72, 73, 81\\ C_{8}: 2, 4, 6, 8, 9, 12, 16, 24, 30, 32, 38, 41, 48, 60, 64, 65, 70, 76, 80, 88, 96, 97\\\]I’m not sure there’s an immediate pattern that is easy to recognize for any of these classes…