Which Collatz numbers do Busy Beavers simulate (if any)?
For context, Collatz’s Tape is introduced in a post prior for instance. In this one, a small modification is made on top of it.
The following is a comparison between the tape development generated by $n = 371581$ (left - using Collatz’s Tape; to be described in a bit) and $\mathbf{BB(4)}$ (right - using the Turing Machine: 1RB1LB_1LA0LC_1RH1LD_1RD0RA):

The tape on the left is generated in the following manner:
- You consider an empty tape with all unmarked cells, such that the reading head (standing initially in the middle of the tape) applies the collatz function to a starting $n$:
flipping the state of the cell it currently stands at (at position $x$) in the following manner:
\[S(x) = \begin{cases} 0 & \text{if} \quad n \equiv 0 \quad (\text{mod}\, 3) \\ 1 - S(x) & \text{if} \quad n \equiv 1 \quad (\text{mod}\, 3) \\ 1 & \text{if} \quad n \equiv 2 \quad (\text{mod}\, 3) \\ \end{cases}\]Additionally, the reading head moves left if $n$ is odd, and right if $n$ is even. It will do this until $n = 1$ is reached. The tape development can then be seen over time (↓). E.g. $n = 10^{20}$:

Albeit, there are vast differences between the examples shown initially, this comparison was made because it’s known that many Busy Beaver champions (and candidates) display Collatz-like behaviour.
- However, do (should) Busy Beavers themselves simulate any Collatz number(s) (using the version of Collatz’s Tape displayed before)?
(Un)related interesting Collatz tapes
| n | CT(n) |
|---|---|
| $10^{20} + 2$ | 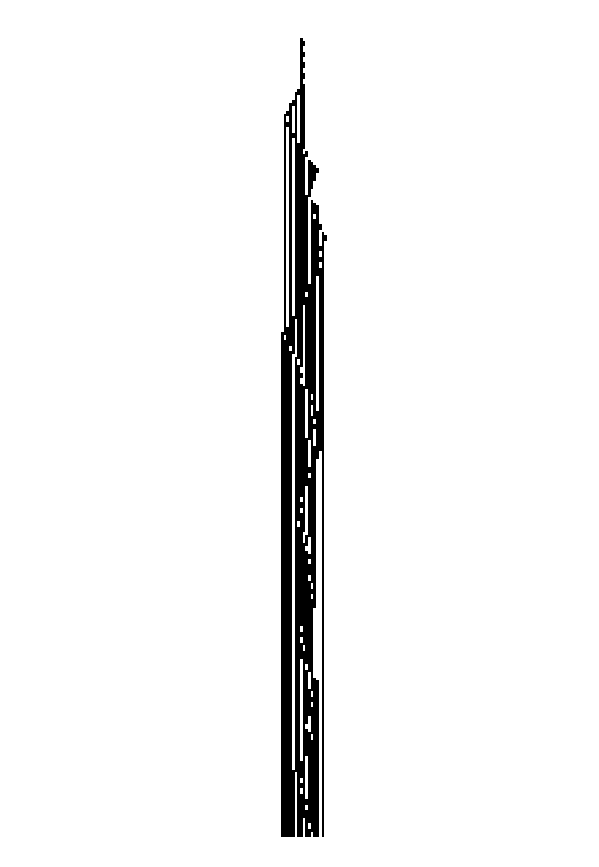 |
| $10^{20} - 1$ |  |
| $10^{25}$ |  |
| $10^{25} - 1$ |  |
| $10^{70}$ |  |