Collatz stopping time parity
Consider the following collatz function:
\[f(n) = \begin{cases} n/2 & \text{if} \quad n \equiv 0 \quad (\text{mod}\, 2) \\ (3n + 1)/2 & \text{if} \quad n \equiv 1 \quad (\text{mod}\, 2) \\ \end{cases}\]and another function which takes as an input the stopping time $τ$ for a given $n$:
\[\omega(n) = \begin{cases} +1 & \text{if} \quad \tau \equiv 0 \quad (\text{mod}\, 2) \\ -1 & \text{if} \quad \tau \equiv 1 \quad (\text{mod}\, 2) \\ \end{cases}\]What should be the behaviour of $\sum_{i = 2}^{\infty} \omega(i)$? Consider it from $n = 2$ to $n = 10^6$:
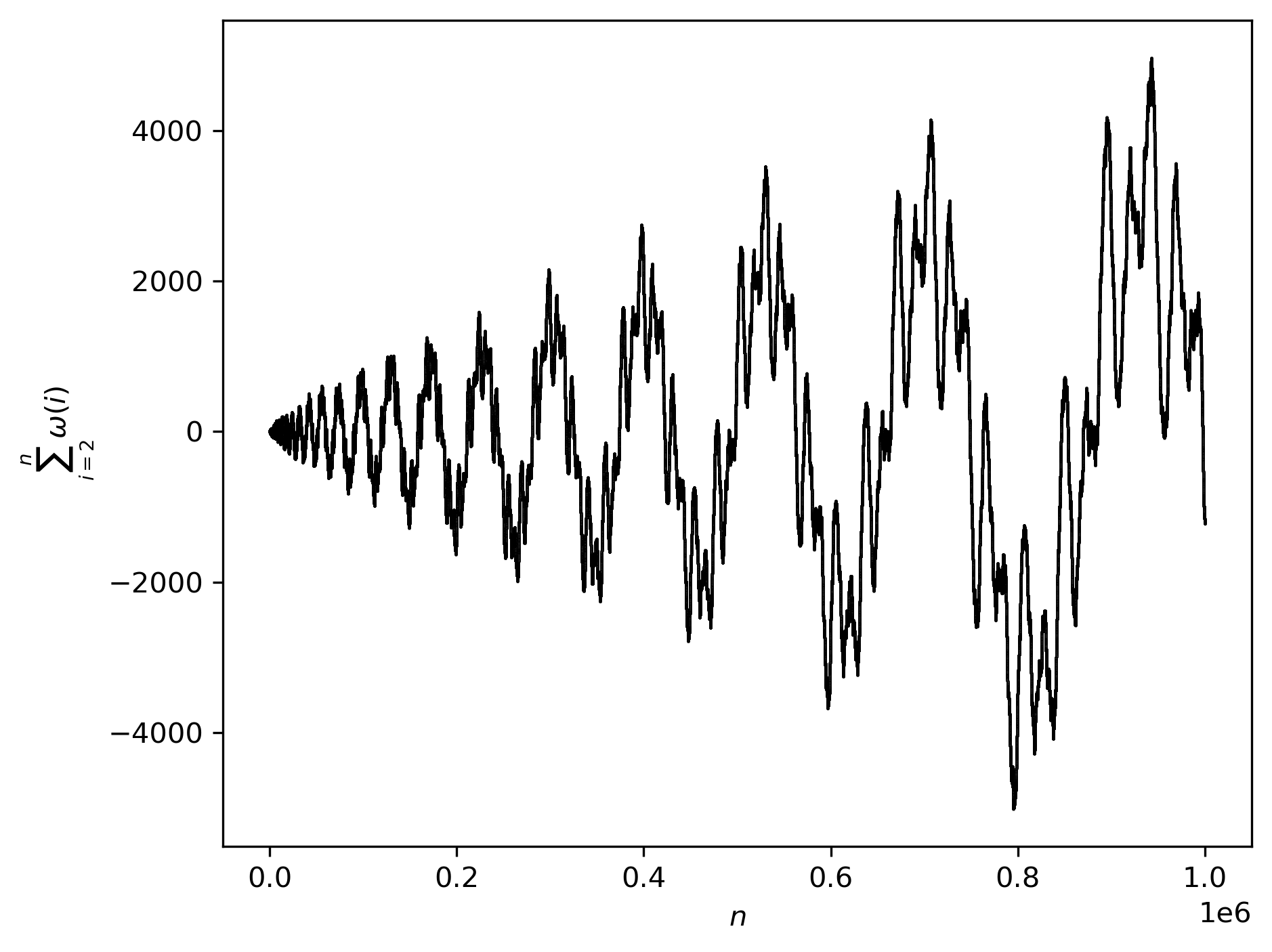
Question: Should $\sum_{i = 2}^{\infty} \omega(i)$ be bounded?