Collatz's Ant - alternative representation of collatz dynamics
Preceding posts here and here.
Consider the example of the landscape of $n = 10^{20} + 99$:

along with the development of its trajectory:

And this is what both the position (euclidean distance) and angle (rads) with respect to the origin look like over time:
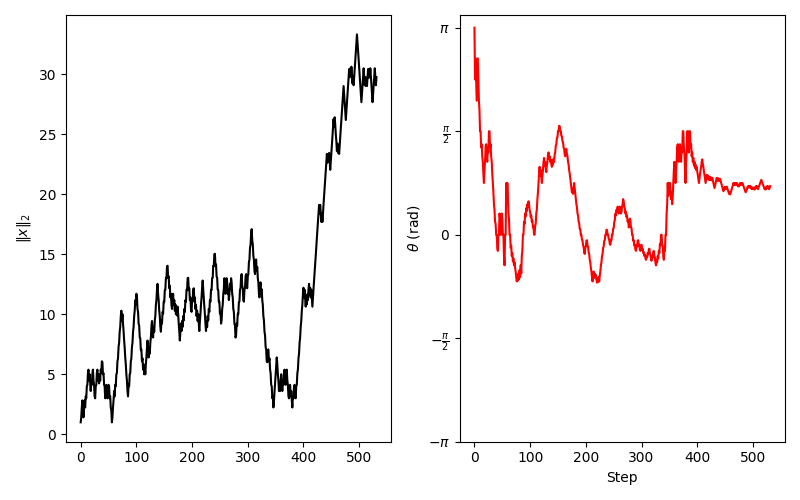
Let’s us forget for a moment that we are talking about a different representation of collatz dynamics for each $n$, based on Langton’s Ant.
Imagine you’re given a set of landscapes (peek at last post for a variety of examples), along with the corresponding trajectories’ development, and some plotting of distance and angles with respect to the origin over time. The only thing you have associated to each of these is the corresponding number $n$. You have purposefully forgotten anything to do with the collatz function itself. You see some systems which could presumably be modelled after random walks (majority of examples by needing to add some drift term). Additionally, you start noticing that a good chunk of these landscapes correspond to the same form, even if with minute differences.
The question is:
- Could one explain the specificity of each landscape (as in the form produced), and how $n$ influences it, without relying on any contextualization with the collatz function?