num(n), Σ(n), space(n), $τ_{n}$, Collatz's Ant and a few other things
Update (July 11, 2025): Small addition regarding the 1D case - Collatz’s Tape.
Previous related posts here, here, here and here.
Let’s take into account a few functions (with some modifications) as defined initially in Tibor Randó’s “On Non-Computable Functions” (1962) in the context of the Busy Beaver problem, and a few additional ones as for instance described here. These are defined within the context of Collatz’s Ant, which may be considered as a 2D tape representation of the dynamics of the collatz function, likewise not being able to be considered as a Turing machine, as the tape (and corresponding symbols marked on it) don’t affect state-transition:
- $\textrm{num}(n)$ is defined as the maximum number of contiguous 1’s (or marked states) left in the 2D tape by the corresponding ant (at the end of the run). The contiguousness is evaluated by the following neighborhood
such that diagonal neighbors aren’t considered valid.
-
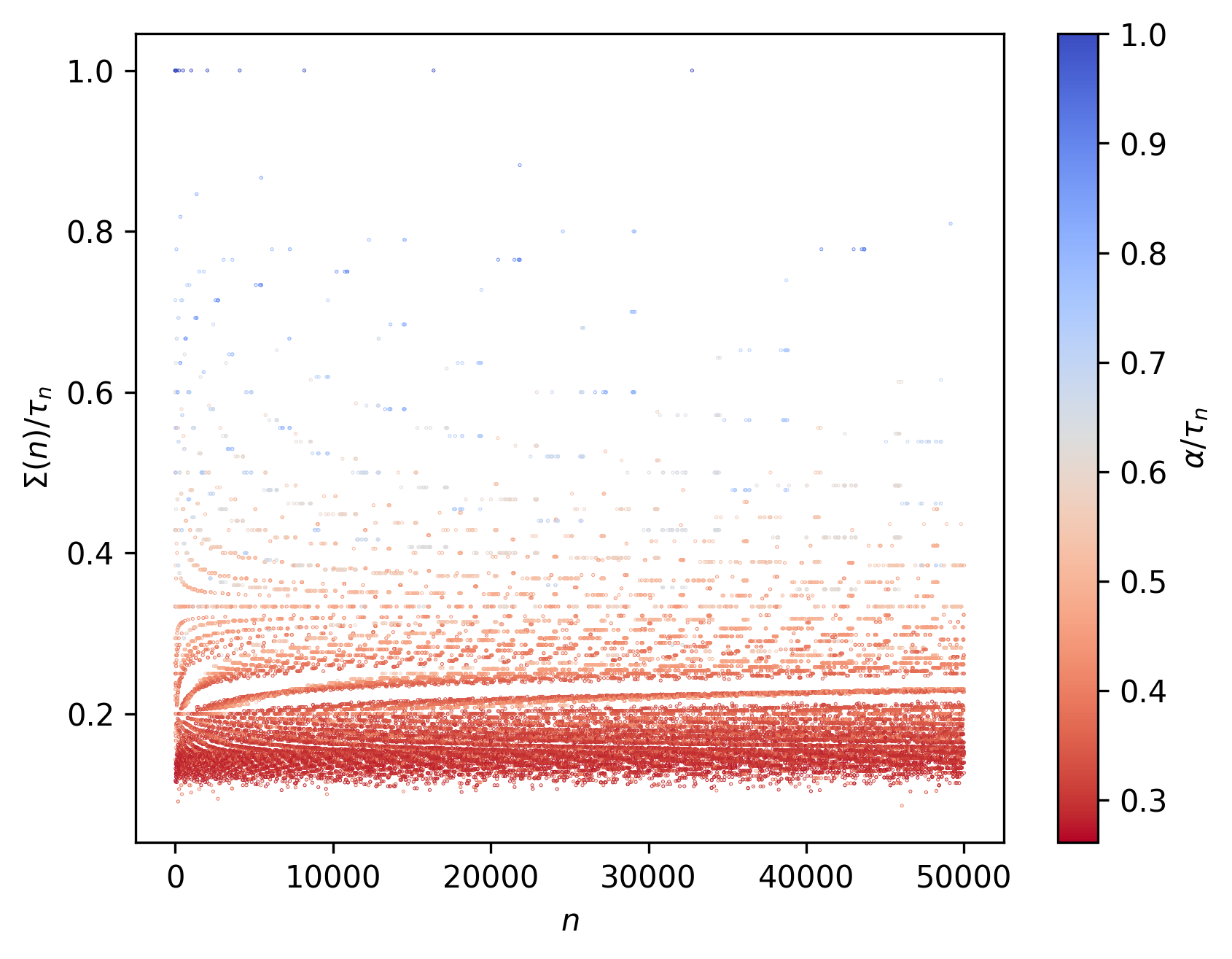
The score function $Σ(n)$ returns the number of 1’s (or marked states) left by the ant on the corresponding landscape or 2D tape, at the end of the run. Two alternative equivalent representations $Σ(n)$ and $Σ(n)^{last}$ might be used, the latter to distinguish from $Σ(n)^{max}$ which represents the maximum amount of marked states left by the ant at any iteration.
-
$\textrm{space}(n)$ represents the number of unique tape cells the corresponding ant visits throughout the run.
and
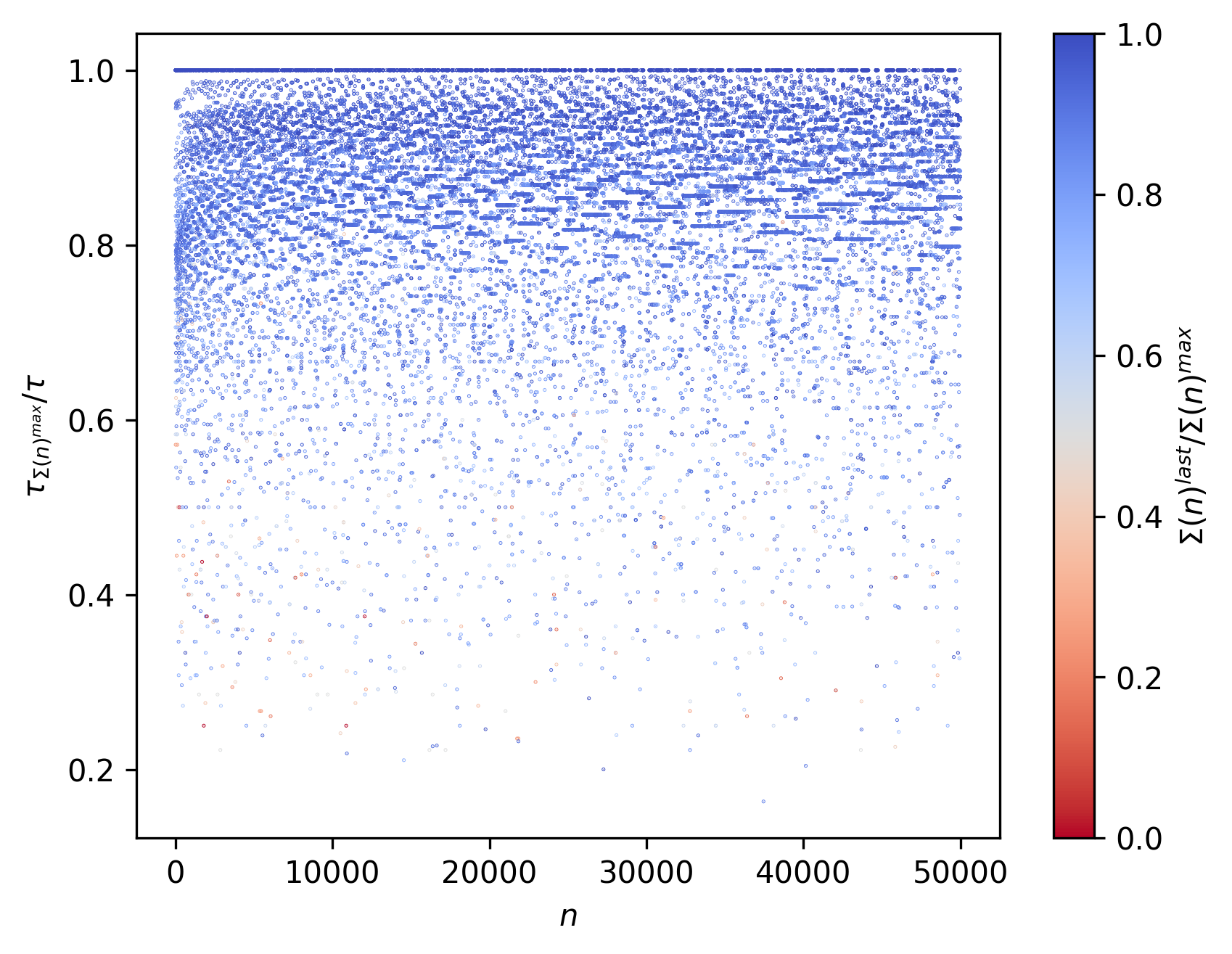
- $\tau_{n}$ (in an analogous manner to the shift function $s(M)$) represents the stopping time or the amount of steps taken by the ant, this being completely dictated by the collatz function.
As with the corresponding 1D representation, the following relations also hold in the 2D case:
\[\textrm{num}(n) ≤ \Sigma(n) ≤ \textrm{space}(n) ≤ \tau_{n}\]Furthermore, we might also want to consider two other metrics (as introduced in previous posts):
-
$\gamma$ gives the (euclidean) distance the ant has relative to the origin at the end of the run.
-
$α$ gives the maximum (euclidean) distance reached relative to the origin over the whole development of the landscape.
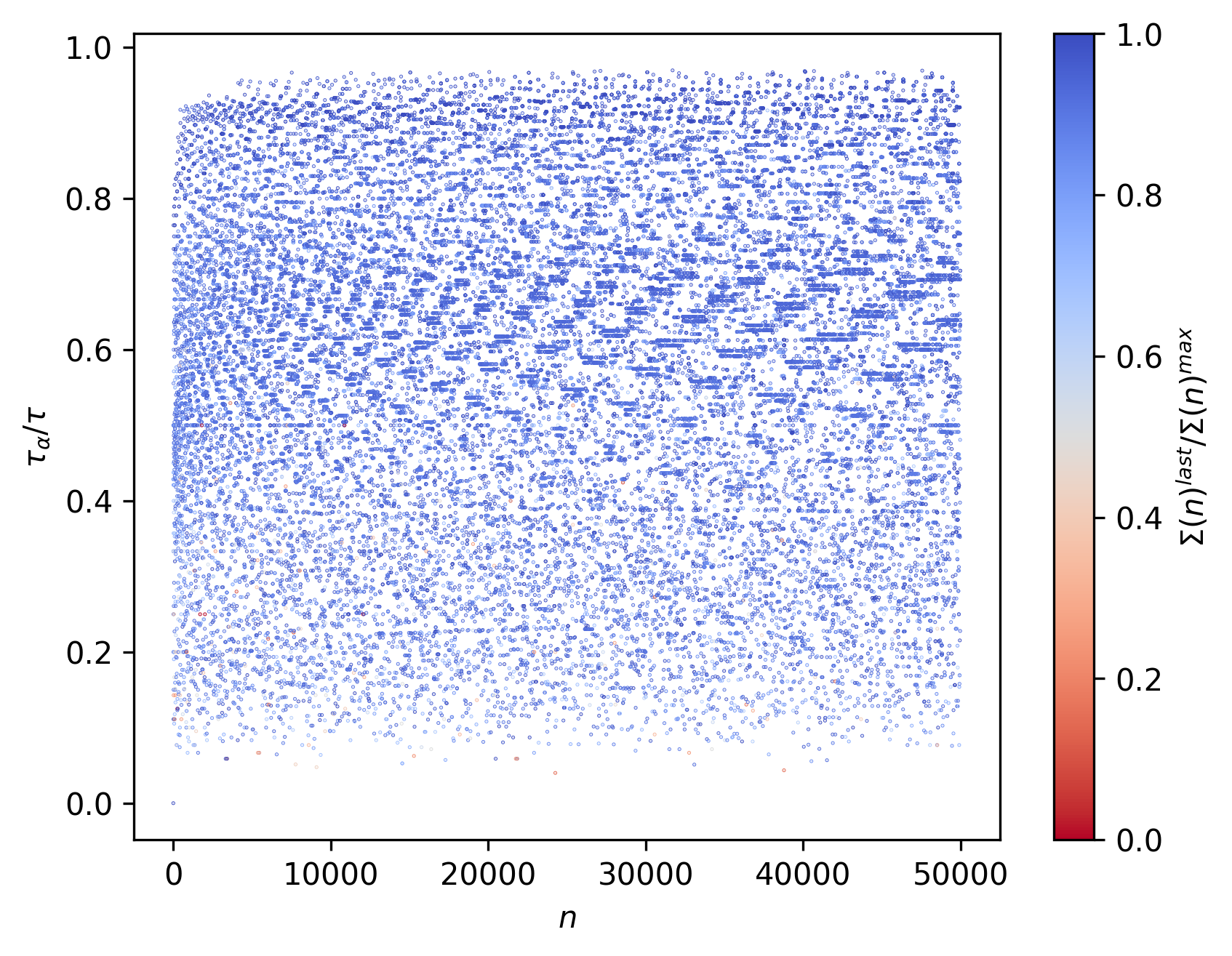
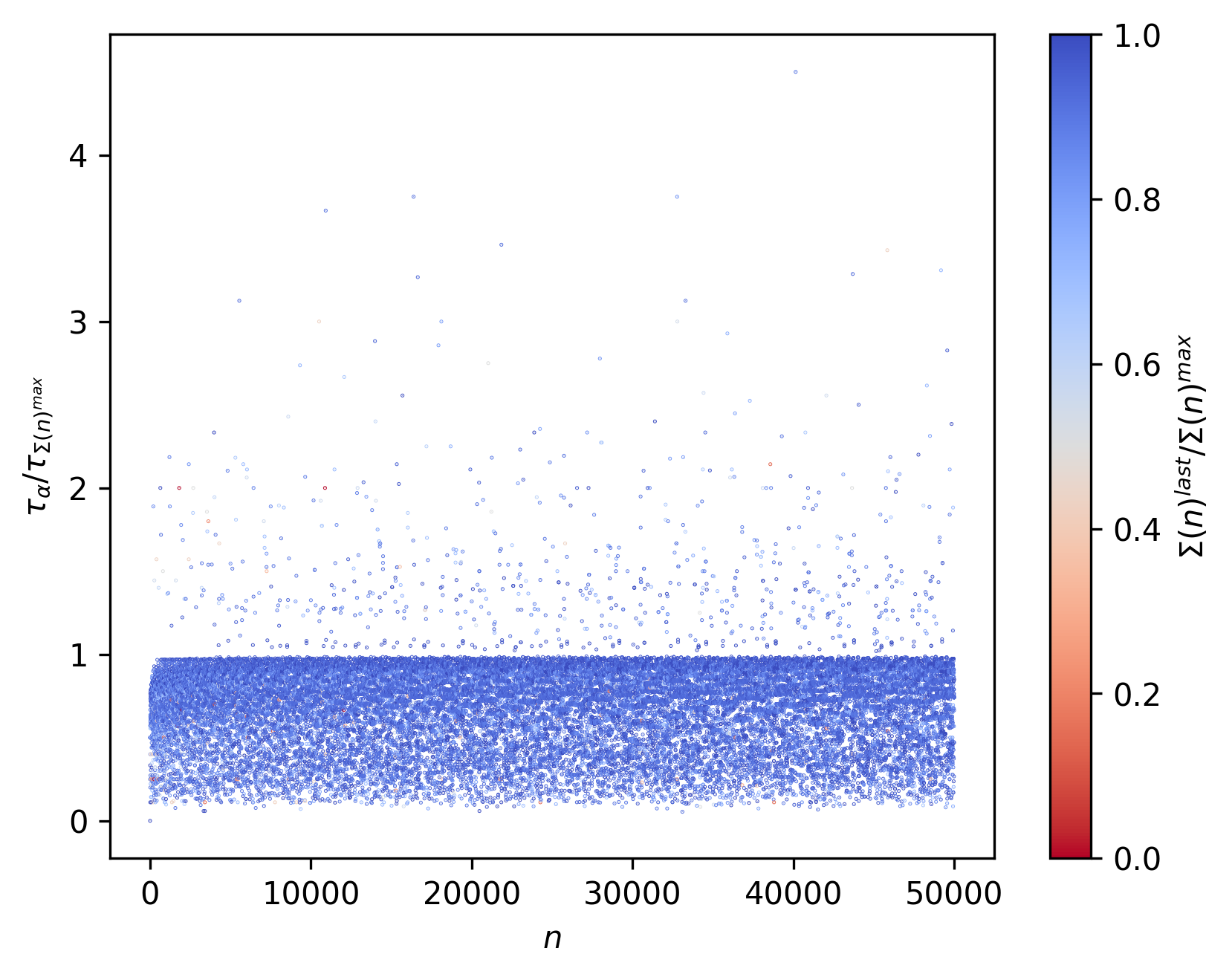
Consider now the following representations from $n = 2$ to $n = 50000$:
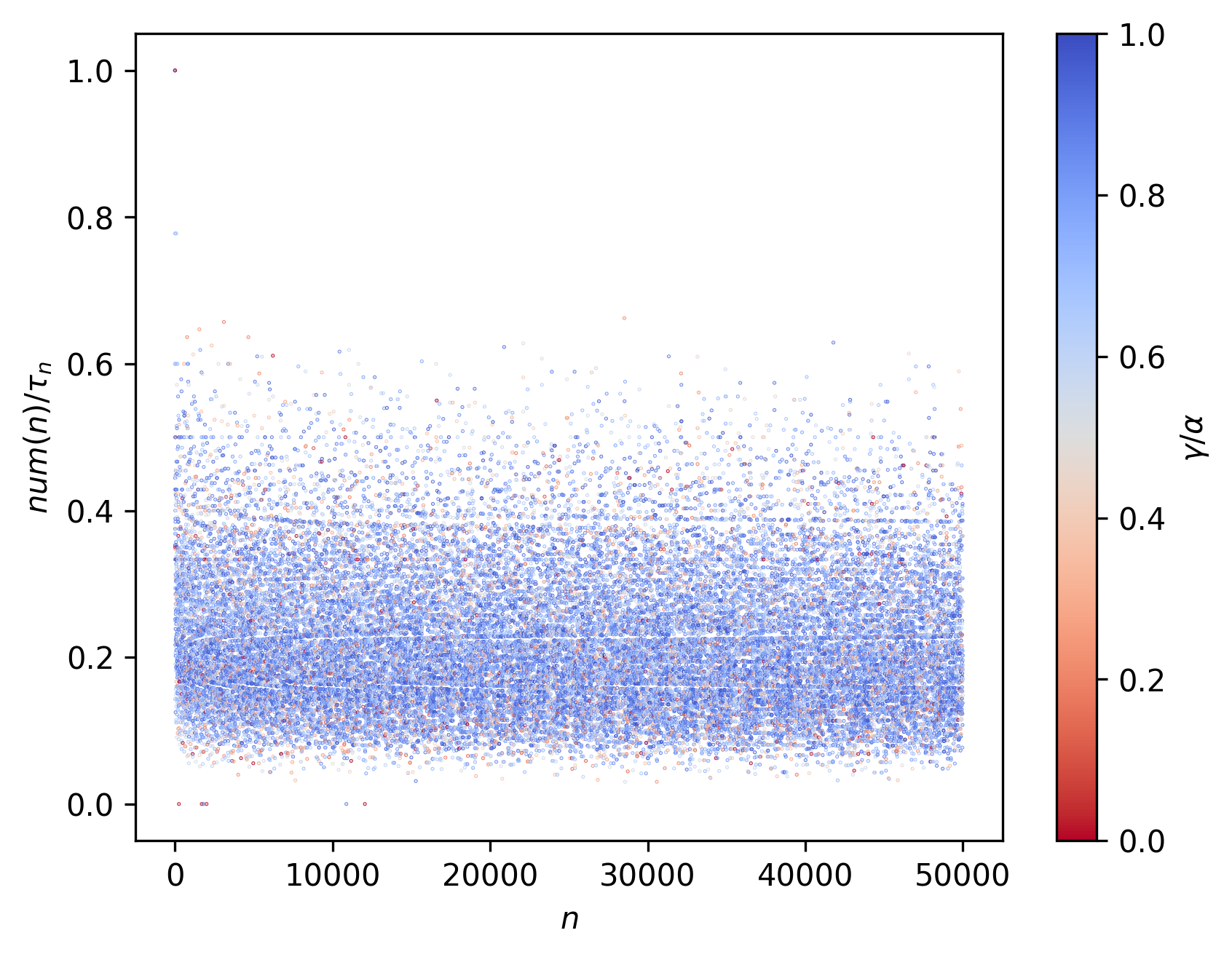
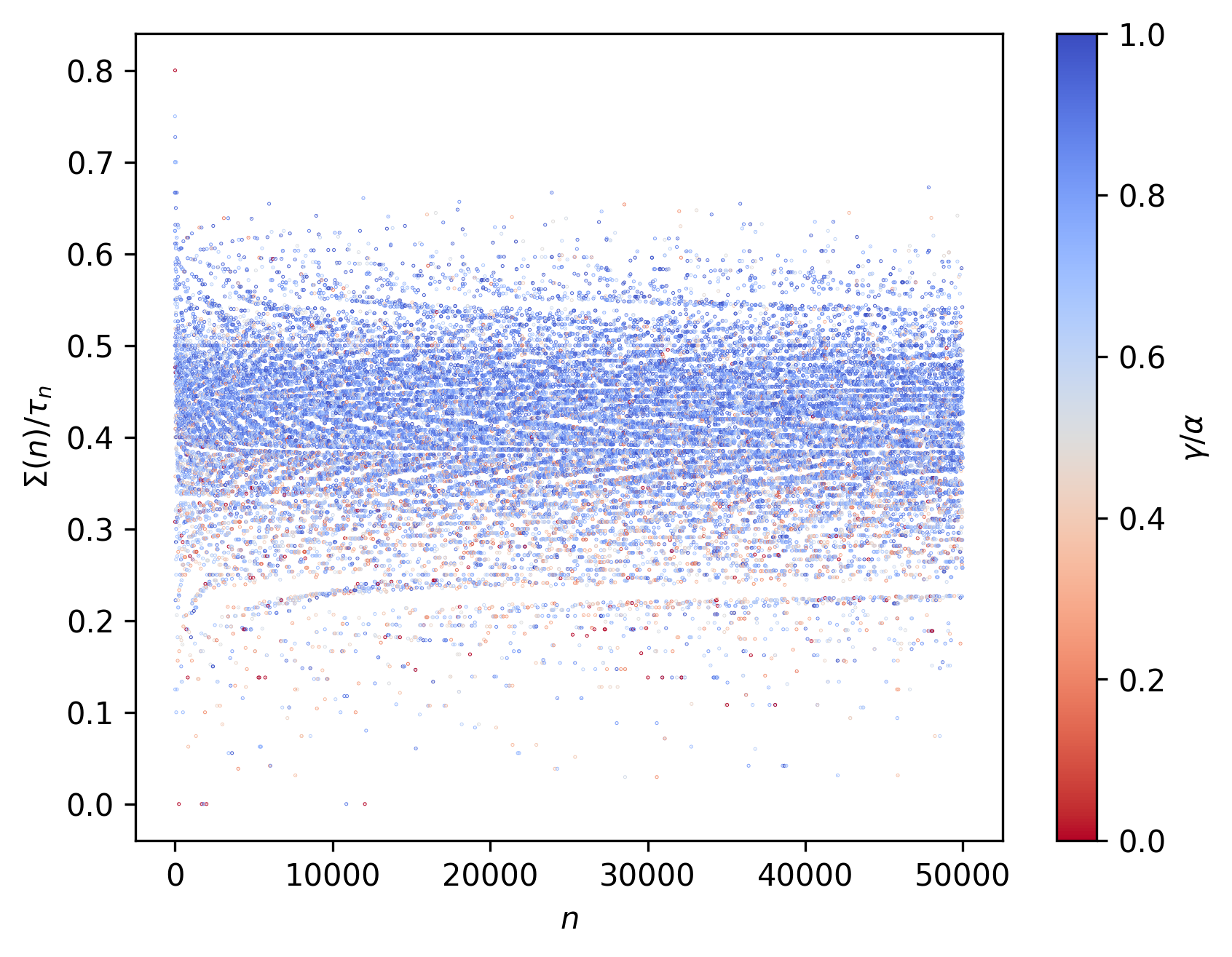
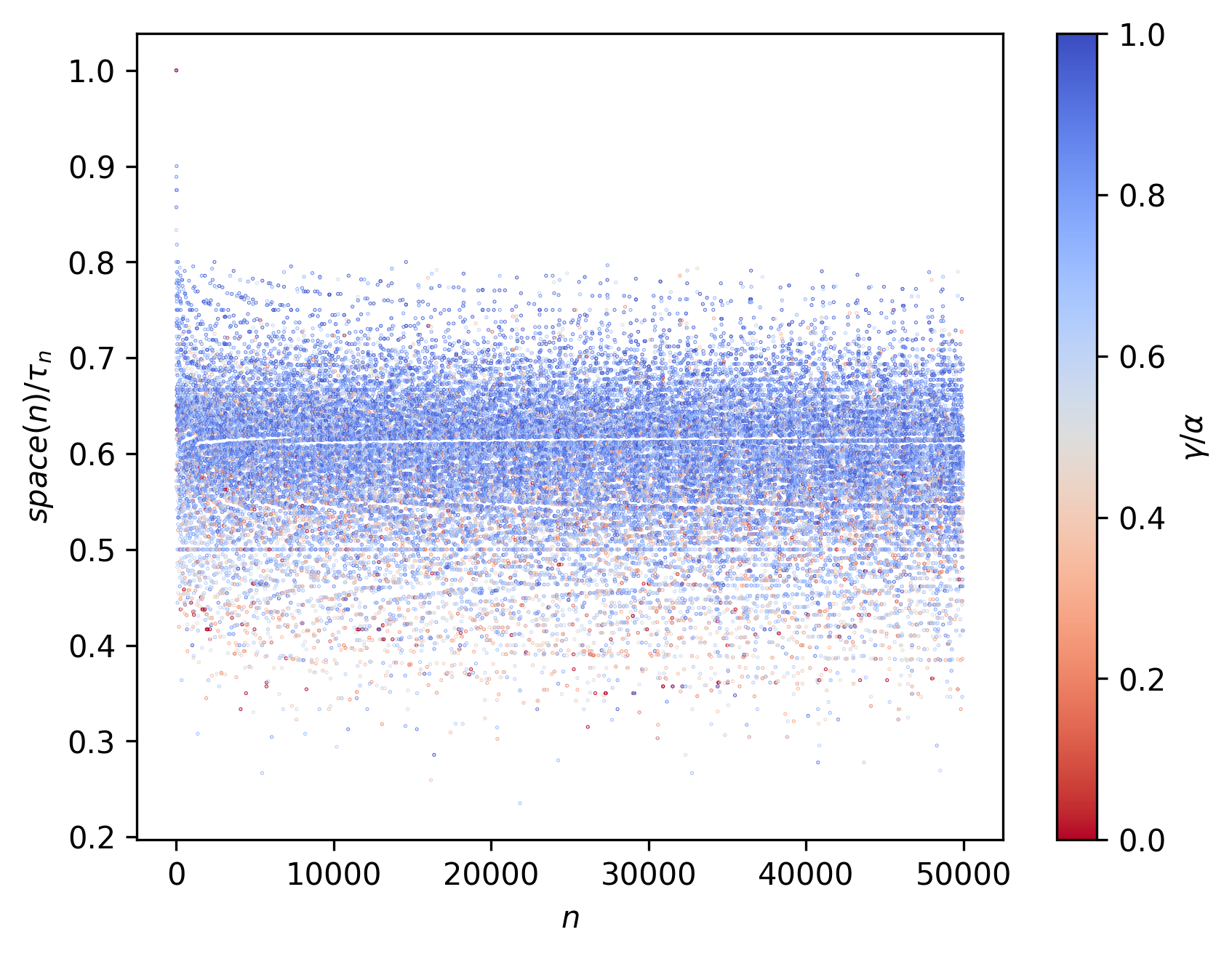
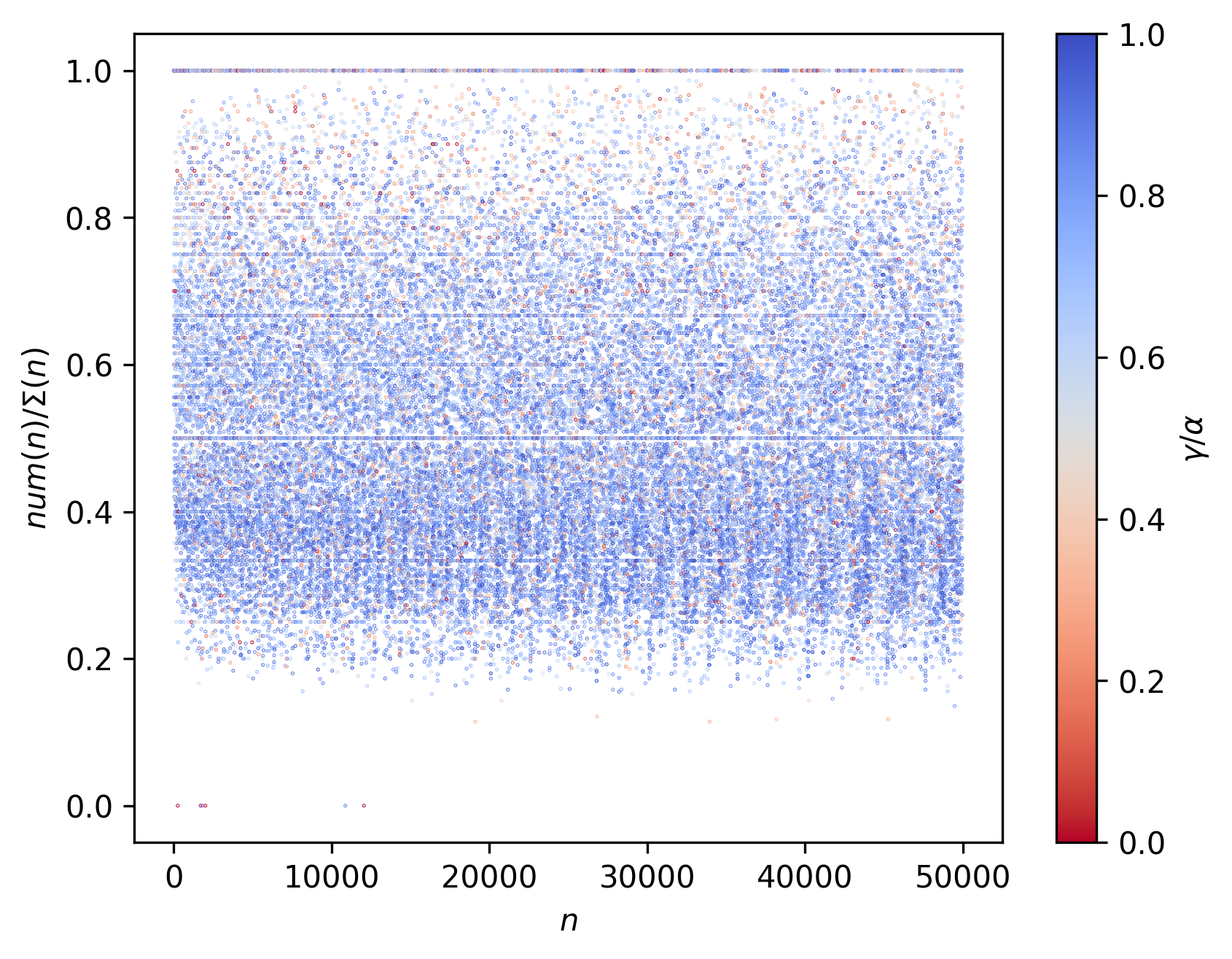
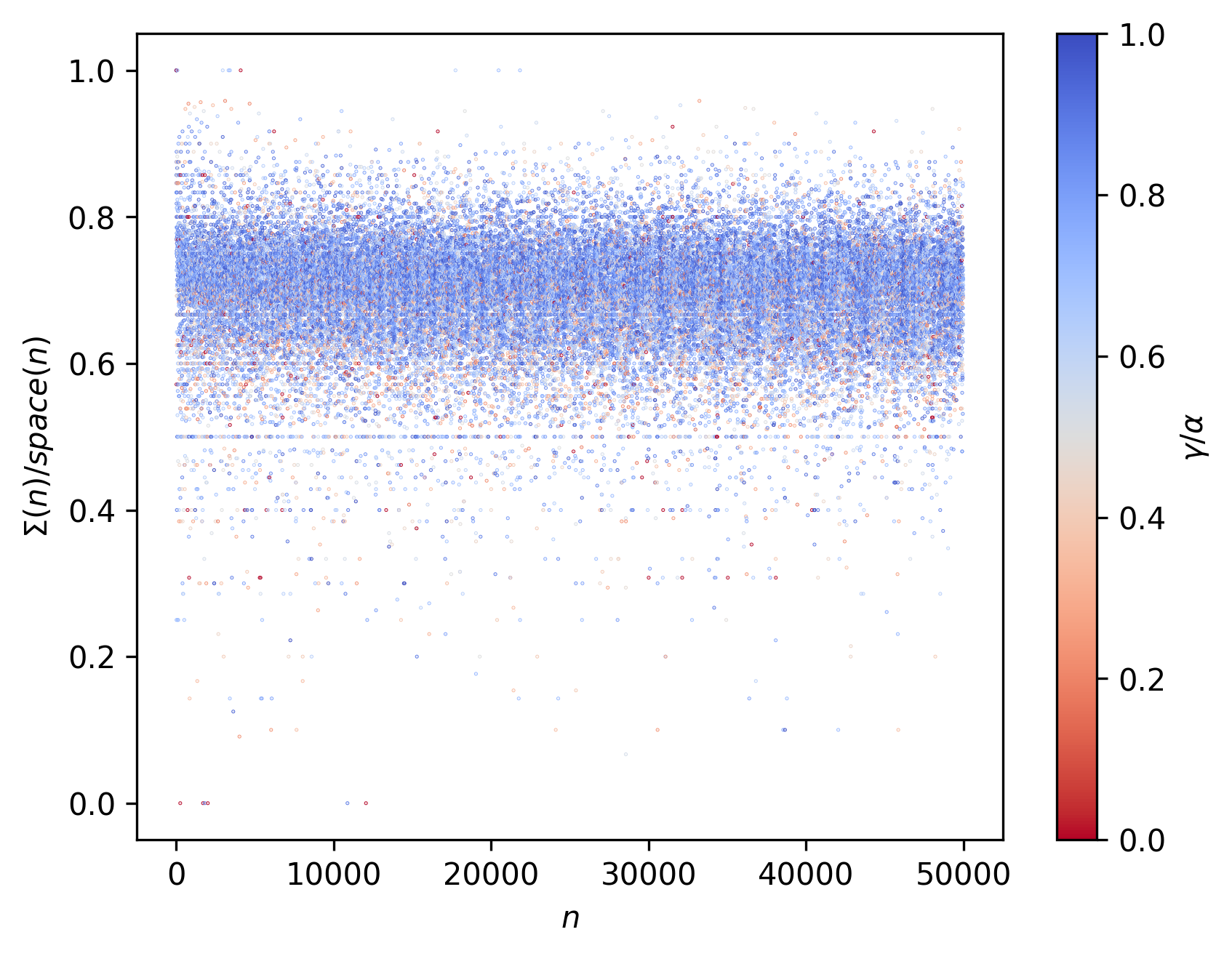
Here $n_{Σ(n)^{max}}$ represents the $n$ at which $Σ(n)$ is first maximized. $n_{max}$ represents maximum $n$ achieved in the corresponding collatz sequence.

Likewise here, $\tau_{Σ(n)^{max}}$ represents the step at which $Σ(n)$ is first maximized, and $τ$ represents the total stopping time.
In a similar fashion, $n_{\alpha}$ represents the $n$ at which $\alpha$ is first achieved.
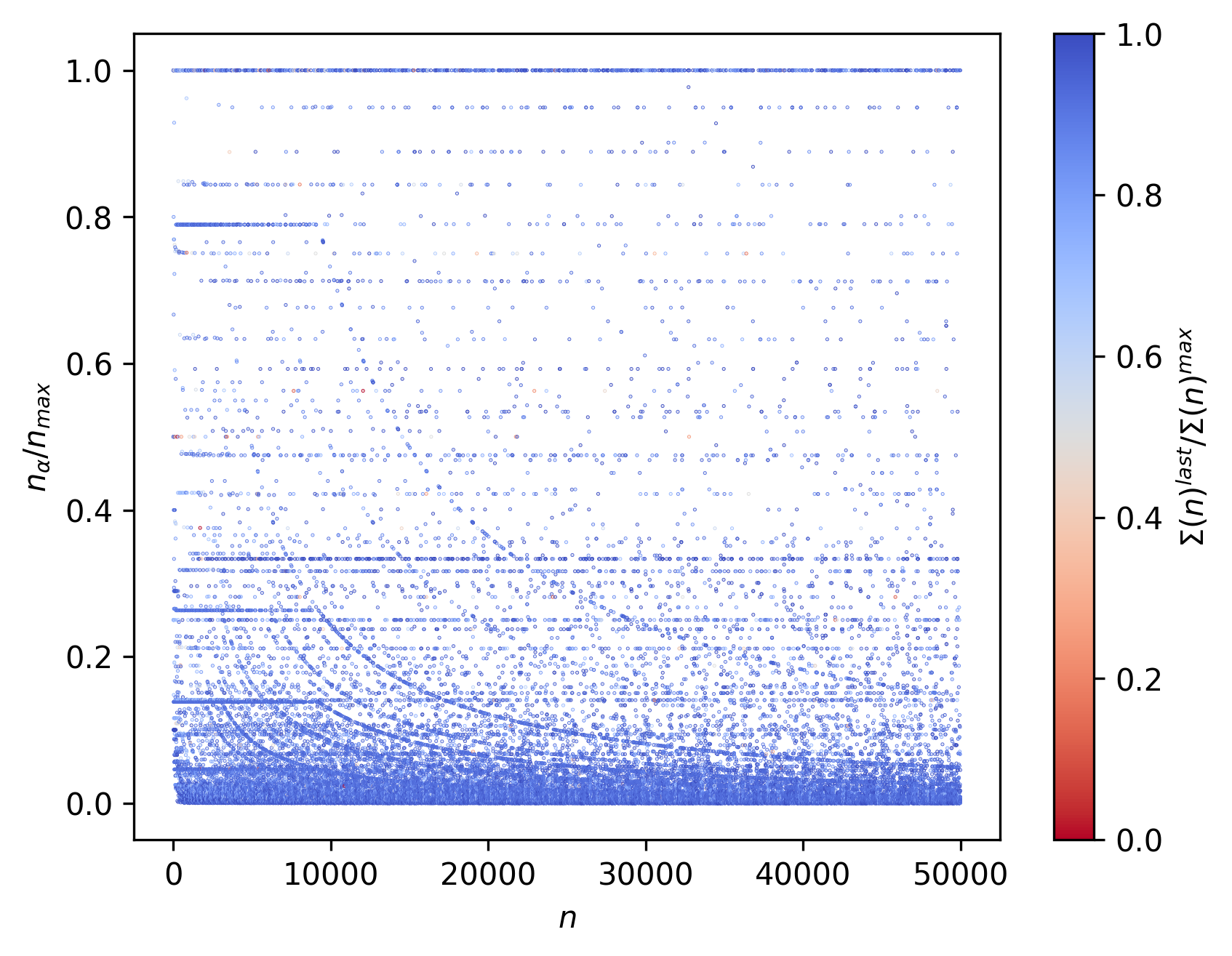
In the same manner, $τ_{\alpha}$ represents the step at which $\alpha$ is first achieved.
Self-cleaning ants related
Regarding the list presented in the last post from $n = 2$ to $n = 10^{6}$, it has been extended to $n = 5 × 10^{6}$:
- Powers of 2 marked with *
| $n$ | $τ_{n}$ |
|---|---|
| 256* | 8 |
| 1704 | 16 |
| 1813 | 16 |
| 2009 | 24 |
| 10880 | 16 |
| 12056 | 24 |
| 65536* | 16 |
| 72808 | 24 |
| 72817 | 24 |
| 77136 | 24 |
| 85717 | 32 |
| 91744 | 32 |
| 101581 | 40 |
| 436224 | 24 |
| 436904 | 24 |
| 464128 | 24 |
| 464213 | 24 |
| 465568 | 24 |
| 504712 | 32 |
| 514304 | 32 |
| 514389 | 32 |
| 548400 | 32 |
| 548557 | 32 |
| 586561 | 40 |
| 609488 | 40 |
| 609745 | 40 |
| 785605 | 56 |
| 2785280 | 24 |
| 2796160 | 24 |
| 3086336 | 32 |
| 3087016 | 32 |
| 3106432 | 32 |
| 3291344 | 32 |
| 3300000 | 32 |
| 3300917 | 32 |
| 3519368 | 40 |
| 3589034 | 40 |
| 3623897 | 40 |
| 3657040 | 40 |
| 3658472 | 40 |
| 3658481 | 40 |
| 3681506 | 40 |
| 3914368 | 40 |
| 4294792 | 48 |
| 4639173 | 48 |
| 4642932 | 56 |
| 4713632 | 56 |
with 20 additional self-cleaning ants. As such, only 47 within this range.
We may also consider the opposite of self-cleaning ants (with $Σ(n) = 0$): dirty ants for which no marked state is flipped again into an un-marked one. The are only 4 examples of dirty ants (with $Σ(n)/τ_{n} = 1$): $n = 2, 4, 8$ and $16$. Presumably only ants which would be counter-examples that shoot up to infinity (and only those with very specific properties with regards to odd-even sequence steps) could be classified as dirty ants. No other ants which halt (and which fall into the trivial attractor) would have $Σ(n)/τ_{n} = 1$, as you are guaranteed to have 4 even reduction steps (accounting for a full rotation of the ant), which will always unmark at least the tape cell the ant originally came from.
Collatz’s Tape
One can also consider the 1D case, with just a small amount of modifications (e.g. right shift when even, left shift when odd), as present in the following script, and with corresponding adaptations in the functions mentioned prior. Consider again the normalized scores, $\Sigma(n)/\tau_{n}$, for $n = 2$ to $n = 50000$: