Collatz's Tape

Let’s develop a bit on the already alluded 1D case of Collatz’s Ant - Collatz’s Tape.

Consider an empty tape with all unmarked cells, such that the reading head (standing initially in the middle of the tape) applies the collatz function to a starting $n$:

flipping the state of the cell it currently stands in, and then moving left if $n$ is odd, and right if $n$ is even. It will do this until $n = 1$ is reached. Consider the example of $n = 27$:

Let us get three values from corresponding tapes:

• $\tau$ is the stopping time for a given $n$ which in this case is completely dictated by the collatz function.

• $\Sigma$ is a score fuction which returns the amount of 1’s (or marked states) left in the tape after $\tau$ iterations. Any explicit deviations from this definition will be mentioned later (e.g. $\Sigma^{max}$).

and

• $α$ is the maximum distance reached relative to the starting position.

For the prior example of $n = 27$, we have $τ = 111$, $Σ = 13$ and $α = 29$.

Just to have an idea of how these vary over $n$, let’s consider the cases from $n = 2$ to $n = 50000$:

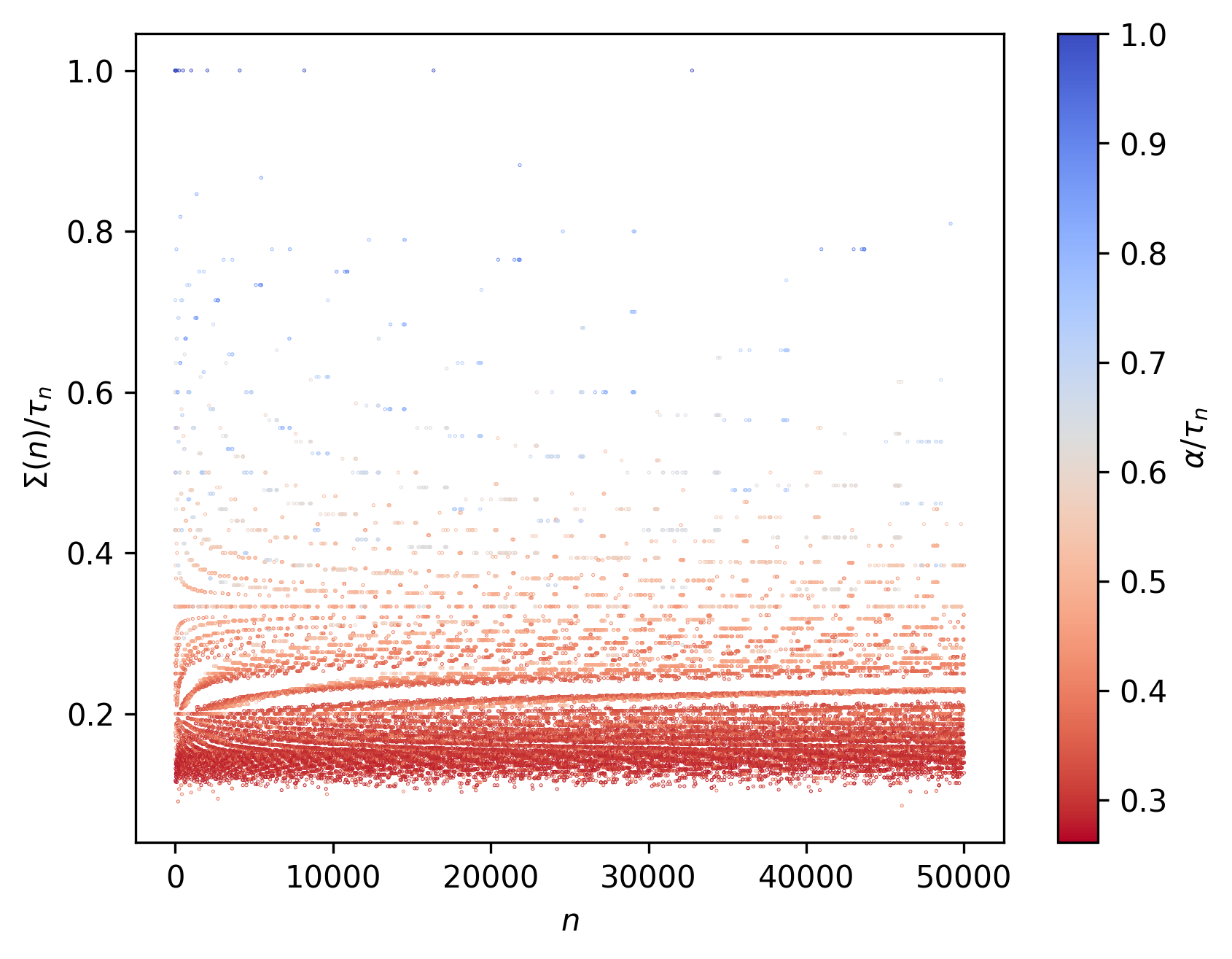
Besides these normalized scores ($\Sigma(n)/\tau_{n}$), we might also want to see at which $n$ is the scoring function first $\Sigma$ maximized ($\Sigma(n)^{max}$) and at which corresponding iteration ($\tau_{\Sigma(n)^{max}}$) does that happen. Here $n_{max}$ represents the maximum $n$ reached by the corresponding collatz function application:

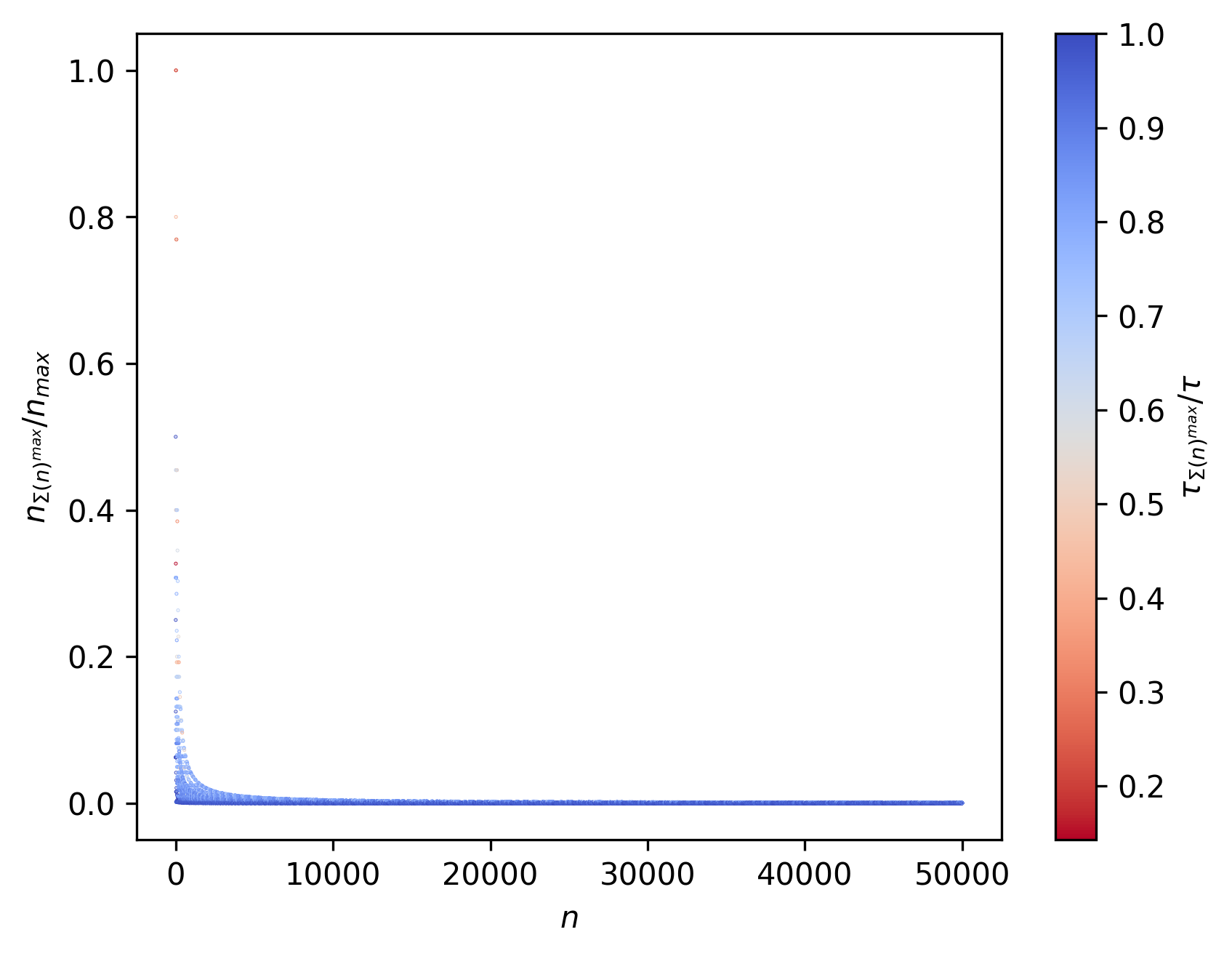
I was interested in seeing this for the 1D case, as the 2D’s case was rather interesting (albeit the color bar isn’t representing the same thing):

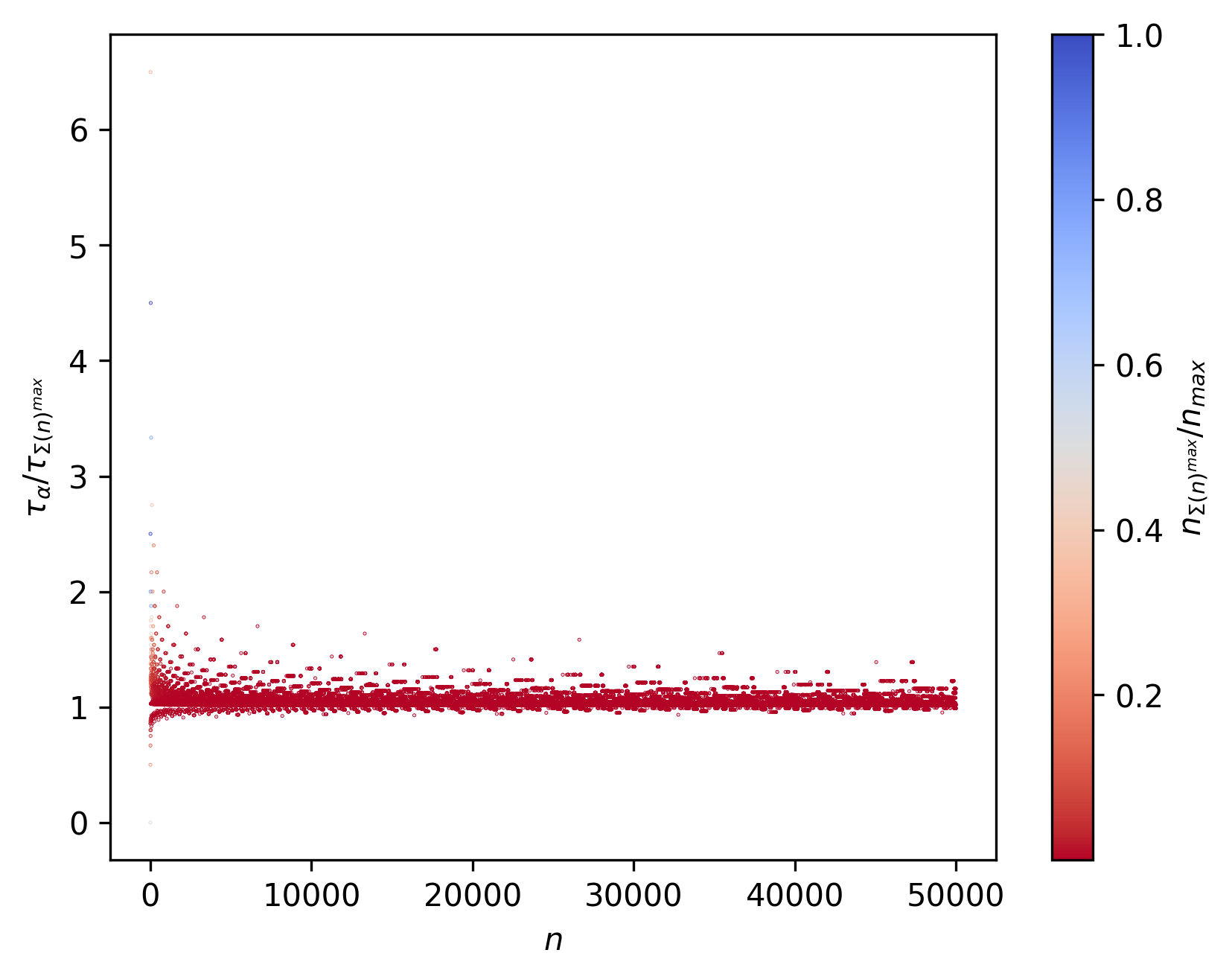
And back to the 1D case, here $\tau_{α}$ represents the step at which $α$ is first reached:

But this setup seems a bit boring… What if the tape itself, and the symbols marked on it, could affect the collatz dynamics?

Collatz’s Tape Machine

Let’s consider a slightly different setup. Everything stays the same, but if the tape reading head happens to shift into a tape cell which is marked (on state - 1), then $n$ is incremented by $1$.

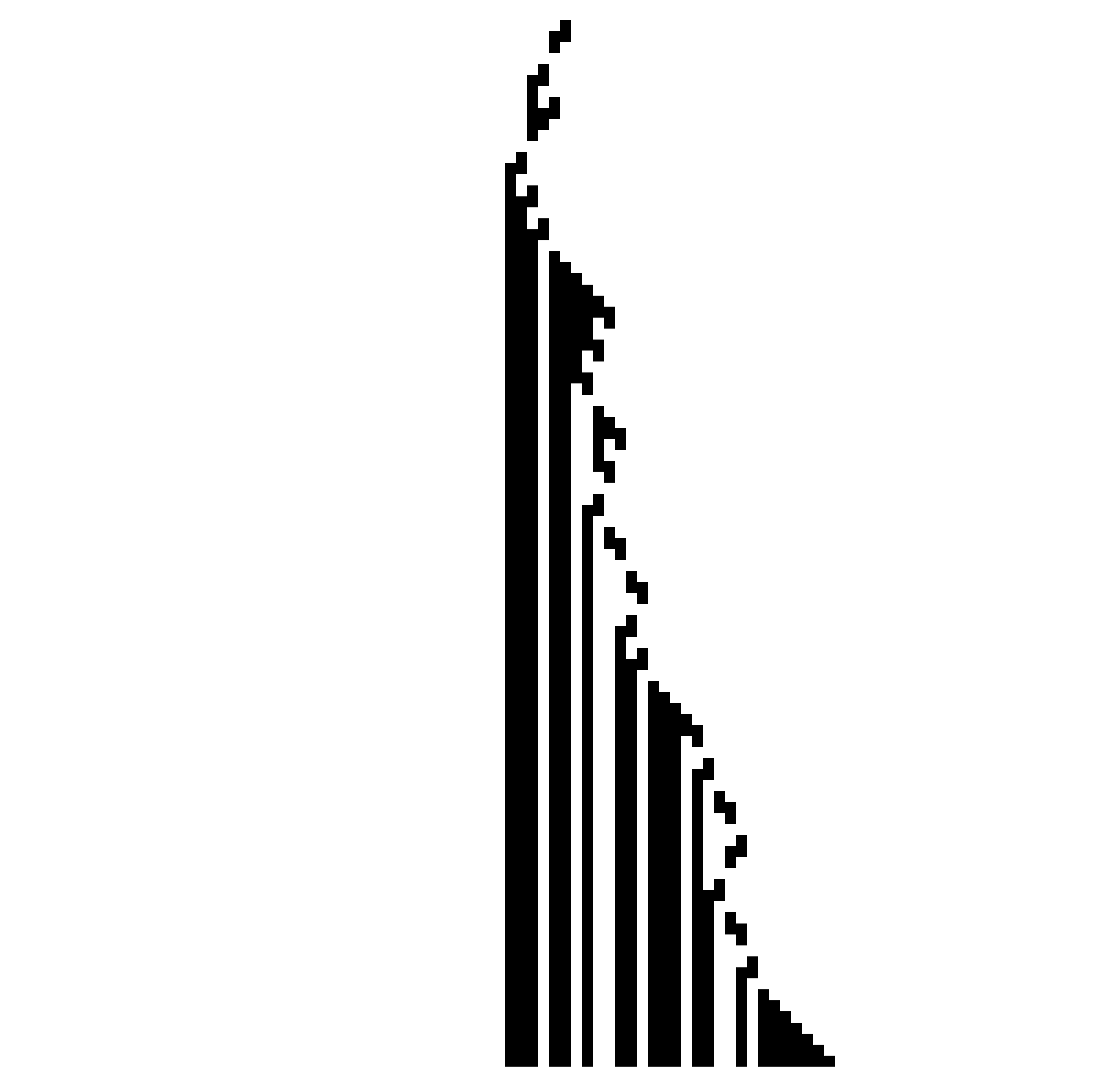
Remember $n = 27$? This is it now:

Or at least the first 200 steps, as it doesn’t seem to halt. And its tape development over each step ($\downarrow$):

For some cases it’s very easy to verify (non)halting behaviour. Consider another non-halting case $n = 5$:

and more importantly its tape development:

We see that there’s cycling behaviour regarding the $n$s, but also that each $n$ is always going to be associated and lead to the same interaction of (un)marking on its neighborhood (regarding where the tape reading head currently stands). So equivalence of states, and therefore a way to verify if there’s cycling behaviour, would need to take this into account.

All of the cases which will be shown and addressed were verified for a tape of finite size and for a limited amount of steps (respectively $N = 200$ and $t_{max} = 10^{5}$), but of course these impose severe limitations. A tape too small will lead to interference, and one can’t be assured that a given $n$ will not halt after $t_{max}$. These were selected after seeing that a variation of 2-4 orders of magnitude of $N = 200$ and $t_{max} = 10^{5}$, didn’t change the status of the non-halting cases, but of course we never know if a bigger variation of these might not make a difference. As such, the status for these (non-trivial) cases will be of possible non-halting.

Let’s consider the cases from $n = 2$ to $n = 20$, making a comparison between the initial scheme of Collatz’s Tape (CT) with no dependencies on tape, and that of Collatz’s Tape Machine (CTM), where the non-halting cases will have a figure showing their tape progression:

$n$	CT	CTM
	$\tau$, $\Sigma$	$\tau$, $\Sigma$
2	1, 1	1, 1
3	7, 3	15, 7
4	2, 2	2, 2
5	5, 3
6	8, 4	6, 2
7	16, 4
8	3, 3	3, 3
9	19, 5	6, 4
10	6, 2
11	14, 2
12	9, 5	7, 3
13	9, 3
14	17, 3
15	17, 5
16	4, 4	4, 4
17	12, 4
18	20, 4
19	20, 4	95, 21
20	7, 3

with the special halting case of $n = 19$ with $τ = 95$:

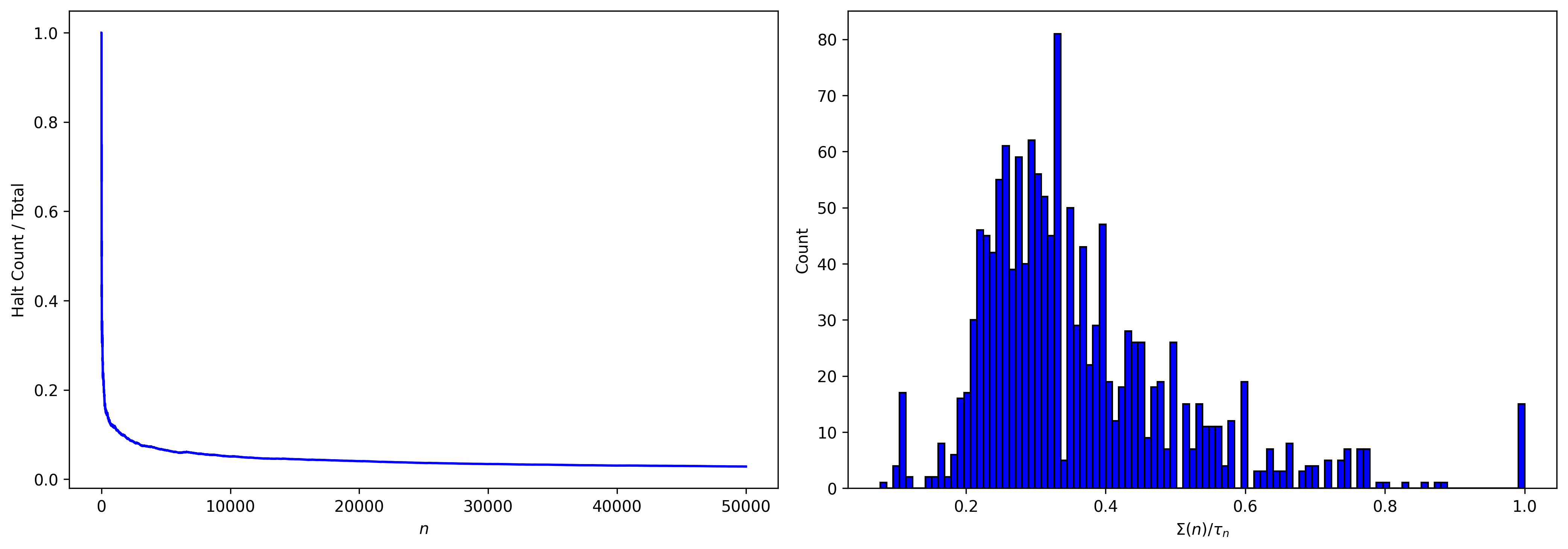
And over the range $n = 2$ to $n = 50000$, we have the following change in the ratio between $n$s which halt and total, along with corresponding distribution of $\Sigma(n)/\tau_{n}$ for the cases which do halt:

Back